Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài AM cắt DC kéo dài tại E
+ Xét tg ABM và tg ECM có
^BAM = ^CEM (góc so le trong)
^AMB = ^CME (góc đối đỉnh)
=> tg ABM đồng dạng tg ECM \(\Rightarrow\frac{BM}{CM}=\frac{AM}{EM}=1\) => M là trung điểm của AE
=> AM là đường cao và đường trung tuyến của tg ADE => tg ADE cân tại D => DM là đường phân giác của ^ADC
A B M D C N
Bài làm:
Gọi N là trung điểm của AD
=> MN là đường trung bình của hình thang ABCD
=> MN // CD => \(\widehat{CDM}=\widehat{NMD}\) (so le trong) (1)
Lại có: MN là đường trung tuyến ứng với cạnh huyền của tam giác vuông AMD
=> \(MN=\frac{AD}{2}=ND\) => Tam giác MND cân tại N
=> \(\widehat{NMD}=\widehat{NDM}\) (2)
Từ (1) và (2) => \(\widehat{CDM}=\widehat{NDM}\)
=> DM là phân giác góc ADC
=> đpcm

ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang

Ta có hình vẽ: A B C D 1 1 2
Ta có: BC= CD (gt)
=> \(\Delta BCD\) cân tại C
=> góc B1 = góc D1
mà góc D1 = D2 (gt)
=> góc D2 = góc B1
mặt khác 2 góc D2 và B1 đang ở vị trí so le trong
=> AB // CD
=> tứ giác ABCD là hình thang

B C D A
Vì BC=CD=>Tam giác BCD cân tại C=>\(\widehat{CBD}=\widehat{CDB}\)(1)
Vì DB là tia phân giác của góc D => \(\widehat{CDB}=\widehat{ADB}\)(2)
Từ (1) và (2) => \(\widehat{CBD}=\widehat{ADB}\),mà 2 góc ở vị trí so le trong
=> AD song song với BC.
=> ABCD là hình thang.

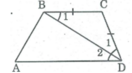
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.
⇒ ∠ B 1 = ∠ D 1 (tính chất tam giác cân)
Mà ∠ D 1 = ∠ D 2 ( Vì DB là tia phân giác của góc D)
Suy ra: ∠ B 1 = ∠ D 2
Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)
Vậy ABCD là hình thang.

Chú ý tam giác CBD cân tại C. Khi đó cùng với DB là phân giác góc S ta chứng minh được A D B ^ = C B D ^