Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vẽ tam giác BDC có BD = 10c,, DC =25cm và BC = 20cm
– Vẽ DC = 25 cm
– Vẽ đường tròn tâm D, bán kính R = 10cm và đường tròn tâm C, bán kính R = 20cm và giao điểm của 2 đường tròn trên là điểm B
* Vẽ điểm A: vẽ đường tròn tâm B, bán kính bằng 4 cm và đường tròn tâm D, bán kính bằng 8 cm. Giao điểm của hai đường tròn là A.
Tứ giác ABCD thỏa mãn các điều kiện bài toán.
b) Ta có AB/BD = 4/10 =2/5; BD/DC =10/25=2/5 và AD/BC = 8/20 =2/5
⇒ AB/BD = BD/DC = AD/BC = 2/5 ⇒ ΔABD ∽ ΔBDC
c) Ta có ΔABD ∽ ΔBDC ⇒ góc \(\widehat{ABD}=\widehat{BDC}\) ⇒ AB//DC
a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ đường tròn tâm D có bán kính = 10cm và đường tròn tâm C có bán kính = 20cm. Giao điểm của hai đường tròn là điểm B.
- Vẽ điểm A: Vẽ đường tròn tâm B có bán kính = 4cm và đường tròn tâm D có bán kính = 8cm. Giao điểm của hai đường tròn này là điểm A.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.

A B C D 8 10 20 25
a, - Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
b, Ta có :
\(\frac{AB}{CD}=\frac{4}{10}=\frac{2}{5};\frac{BD}{CD}=\frac{10}{25}=\frac{2}{5};\frac{AD}{BC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}=\frac{AD}{BC}\Rightarrow\Delta ABD~\Delta BDC\left(c-c-c\right)\)
c, \(\Delta ABD~\Delta BDC\)
\(\Rightarrow\widehat{ABD}=\widehat{BDC}\)
Vì 2 góc này so le trong nên
=> AB // DC hay ABCD là hình thang

A B C D 8 25 20 4 10
a, Cách vẽ :
Vẽ tam giác BDC
+) DC = 25cm
+) Vẽ cung tâm tròn D có bán kính 10cm và cung tròn tâm C có bán kính 20cm . Giao điểm của 2 cung tròn là B
- - Vẽ điểm A: Vẽ cung tròn tâm B có bán kính 4cm và cung tròn tâm D có bán kính 8cm. Giao điểm của hai cung tròn này là điểm A. Nối các cạnh BD, BC, DA, BA.
=> Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.
b, Ta có : \(\frac{AB}{BD}=\frac{4}{10}=\frac{2}{5};\frac{BD}{DC}=\frac{10}{25};\frac{AD}{BC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AB}{BD}=\frac{BD}{DC}=\frac{AD}{BC}\)
=> tam giác ABD ∽ tam giác BDC ( c - c - c )
c, Tam giác ABD ∽ tam giác BDC ( theo chứng minh câu b )
\(\Rightarrow\widehat{ABD}=\widehat{BDC}\), mà 2 góc ở vị trí sole trong
\(\Rightarrow AB//DC\)hay ABCD là hình thang

b: Xét ΔABD và ΔBDC có
AB/BD=BD/DC=AD/BC
Do đó: ΔABD\(\sim\)ΔBDC
c: Ta có: ΔABD\(\sim\)ΔBDC
nên \(\widehat{ABD}=\widehat{BDC}\)
=>AB//CD

a) Xét 2 tam giác ADB và BCD có:
góc DAB = góc DBC (gt)
góc ABD = góc BDC ( so le trong )
nên tam giác ADB đồng dạng với tam giác BDC.(1)
b) Từ (1) ta được AB/BC = DB/CD = AB/BD
hay ta có; AD/BC = AB/BD <==> 3,5/BC = 2,5/5
==> BC= 3,5*5/2,5 = 7 (cm)
ta cũng có: DB/CD = AB/BD <==> 5/CD = 2,5/5
==> CD = 5*5/2,5 =10 (cm)
c) Từ (1) ta được;
AD/BC = DB/CD = AB/BD hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .
ta nói tam giác ADB đồng giạc với tam giác BCD theo tỉ số đồng dạng là 1/2
mà tỉ số diện tích bằng bình phương tỉ số động dạng
do đó S ADB/ S BCD = (1/2)^2 = 1/4

Bài 1)
a) Vì A: B:C:D = 1:2:3:4
=> A= B/2 = C/3=D/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
A = 36 độ
B= 72 độ
C=108 độ
D= 144 độ
b) Ta có :
A + D = 36 + 144 = 180 độ(1)
B+C = 72 + 108 = 180 độ(2)
Từ (1) và (2) ta có:
=> AB //CD (dpcm)
c) Ta có :
CDE + ADC = 180 độ(kề bù)
=> CDE = 180 - 144 = 36
Ta có :
BCD + DCE = 180 độ ( kề bù)
=> DCE = 180 - 108 = 72
Xét ∆CDE ta có :
CDE + DCE + DEC = 180 ( tổng 3 góc trong ∆)
=> DEC = 180 - 72 - 36 = 72 độ
Bài 2)
a) Ta có ABCD có :
A + B + C + D = 360 độ
Mà C = 80 độ
D= 70 độ
=> A+ B = 360 - 80 - 70 = 210 độ
Ta có AI là pg góc A
BI là pg góc B
=> DAI = BAI = A/2
=> ABI = CBI = B/2
=> BAI + ABI = A + B /2
=> BAI + ABI = 210/2 = 105
Xét ∆IAB ta có :
IAB + ABI + AIB = 180 độ
=> AIB = 180 - 105
=> AIB = 75 độ
=>
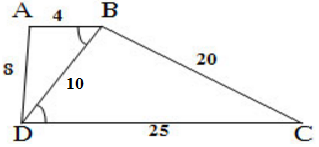

a) Cách vẽ:
- Vẽ ΔBDC:
+ Vẽ DC = 25cm
+ Vẽ cung tròn tâm D có bán kính = 10cm và cung tròn tâm C có bán kính = 20cm. Giao điểm của hai cung tròn là điểm B.
Nối DB và BC.
- Vẽ điểm A: Vẽ cung tròn tâm B có bán kính = 4cm và cung tròn tâm D có bán kính = 8cm. Giao điểm của hai cung tròn này là điểm A.
Nối DA và BA.
Vậy là ta đã vẽ được tứ giác ABCD thỏa mãn điều kiện đề bài.