Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\frac{a}{b+c+d}+1=\frac{b}{a+c+d}+1=\frac{c}{a+b+d}+1=\frac{d}{a+b+c}+1\)
\(\Rightarrow\) \(\frac{a+b+c+d}{b+c+d}=\frac{a+b+c+d}{a+c+d}=\frac{a+b+c+d}{a+b+d}=\frac{a+b+c+d}{a+b+c}\)
Vì \(a+b+c+d\ne0\) nên \(a=b=c=d\)
Do đó: \(M=4\)

Bài 1)
Ta có : A + B + C + D = 360 độ
=> A + B = 140 độ
Ta có :
A = \(\frac{140+40}{2}\)= 90 độ
=> B = 90 - 40 = 50 độ
Bài 1 :
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+120^o+100^o=360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+220^o=360^o\)
\(\Rightarrow\widehat{A}+\widehat{B}=140^o\)
Mà : \(\widehat{A}-\widehat{B}=40^o\)
\(\Rightarrow\widehat{A}+\widehat{A}+\widehat{B}-\widehat{B}=140^o+40^o\)
\(\Rightarrow2\widehat{A}=180^o\Leftrightarrow\widehat{A}=90^o\)
\(\Leftrightarrow\widehat{B}=140^o-\widehat{A}=140^o-90^o=50^o\)
\(KL:\widehat{A}=90^o;\widehat{B}=50^o\)

a) Xét tứ giác ABCD ta có ( ^B = 2^C mới được nhé)
^A + ^B + ^C + ^D = 3600
=> 1500 + ^B + ^C + ^D = 3600
=> ^B + ^C + ^D = 2100
Có ^B = 2^C
=> 2 ^C + ^C + ^D = 2100
=> 3^C + ^D = 2100
Có ^C = 2^D
=> 3 . 2^D + ^D = 2100
=> 7^D = 2100
=> ^D = 300
+) ^C = 2^D = 2.300 = 600
+) ^B = 2^C = 2.600 = 1200
b) Xét tứ giác ABCD có :
^A + ^B + (^C + ^D) = 3600
=> 2^B + ^B + 2100 = 3600
=> 3^B = 1500
=> ^B = 500
+) ^A = 2^B = 2.500 = 1000
Có ^C + ^D = 2100 => ^C = ^D = 210 : 2 = 1050
Vậy ^A = 1000,^B = 500,^C = ^D = 1050
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)
=> ^A = 360 , ^B = 720 , ^C = 1080 , ^D = 1440
d) Tự làm

1. Áp dụng định lý tổng 3 góc vào tam giác ICD , bạn tính được góc ICD +góc IDC = 75 độ
Mà góc BCD = 2 góc ICD và góc ADC = 2 góc IDC nên góc BCD + góc ADC = 2.75 = 150 độ
Xét tứ giác ABCD có: góc A + góc B + góc BCD + góc ADC = 360 độ
góc A + 90 độ + 150 độ = 360 độ
góc A = 120 độ
2. góc C của tứ giác là: 180 độ -130 độ = 50 độ
Chúc bạn học tốt.

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
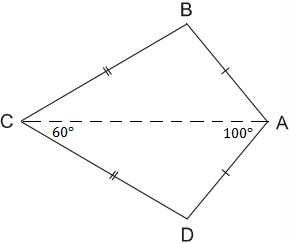
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

nhầm;
lấy (1) , (2), (3) cộng cho nhau:
góc B + góc C = 200o (1)
góc B + góc D = 180o (2)
góc C + góc D = 120o (3)
----------------------------------
2B + 2C + 2D = 5000
=> 2 (B + C + D) = 5000
=> B + C + D = 500 : 2 = 2500
=> Â = 3600 - B + C + D = 3600 - 2500
tới đây hết bít

Ta có: \(F=\frac{a}{b+c}+\frac{b}{c+d}+\frac{c}{d+a}+\frac{d}{a+b}\)
\(\Leftrightarrow F=\frac{a^2}{ab+ac}+\frac{b^2}{bc+bd}+\frac{c^2}{cd+ca}+\frac{d^2}{da+db}\)
\(\Leftrightarrow F\ge\frac{\left(a+b+c+d\right)^2}{2ac+2bd+\left(a+c\right)\left(b+d\right)}=P\)
\(\Leftrightarrow P=\frac{a^2+b^2+c^2+2ab+2bc+2cd+2ad+2ac+2bd}{ab+ac+bc+bd+cd+ac+ad+bd}\)
\(\Leftrightarrow P=\frac{\left(a^2+c^2\right)+\left(b^2+d^2\right)+2ab+2bc+2cd+2ad+2ac+2bd}{2ac+2bd+ab+bc+cd+ad}\)
(Vì \(a^2+c^2\ge2ac\Leftrightarrow\left(a-c\right)^2\ge0\)luôn đúng; \(b^2+d^2\ge2bd\Leftrightarrow\left(b-d\right)^2\ge0\)luôn đúng)
\(\Leftrightarrow P\ge\frac{2ac+2bd+2ab+2bc+2cd+2ad+2ac+2bd}{2ac+2bd+ab+cd+ad+ac+bd}\)
\(\Leftrightarrow P\ge\frac{4ac+4bd+2ab+2bc+2cd+2ad}{2ac+2bd+ab+bc+cd+ad}=2\)
\(\Leftrightarrow F\ge P\ge2\)
\(\LeftrightarrowĐPCM\)
Đáp án cần chọn là: A
Xét tam giác ABC có: B ^ = 100 ° ; A B = B C
⇒ ∆ A B C cân tại B .
B A C ^ = B C A ^ = 180 0 − 100 0 2 = 40 0
Xét tam giác ADC có C D = D A ⇒ ∆ A D C cân tại D có A D C ^ = 70 ° nên D A C ^ = D C A ^ = 180 0 − 70 0 2 = 55 0
Từ đó ta có A ^ = B A D ^ = B A C ^ + C A D ^ = 40 ° + 55 ° = 95 °
Và C ^ = B C D ^ = B C A ^ + A C D ^ = 40 ° + 55 ° = 75 °
Nên A ^ = C ^ = 95 °