
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

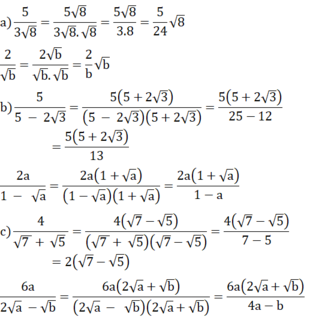

a: \(\dfrac{5}{3\sqrt{8}}=\dfrac{5\sqrt{2}}{3\cdot4}=\dfrac{5\sqrt{2}}{12}\)
\(\dfrac{2}{\sqrt{b}}=\dfrac{2\sqrt{b}}{b}\)
b: \(\dfrac{5}{5-2\sqrt{3}}=\dfrac{25+10\sqrt{3}}{13}\)
\(\dfrac{2a}{1-\sqrt{a}}=\dfrac{2a\left(1+\sqrt{a}\right)}{1-a}\)
c: \(\dfrac{4}{\sqrt{7}+\sqrt{5}}=\dfrac{4\left(\sqrt{7}-\sqrt{5}\right)}{2}=2\sqrt{7}-2\sqrt{5}\)
\(\dfrac{6a}{2\sqrt{a}-\sqrt{b}}=\dfrac{6a\left(2\sqrt{a}+\sqrt{b}\right)}{4a-b}\)

\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}=\dfrac{\left(\sqrt{5}-1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}=\dfrac{5-2\sqrt{5}+1}{5-1}=\dfrac{2\left(3-\sqrt{5}\right)}{4}=\dfrac{3-\sqrt{5}}{2}\)
b: \(\dfrac{37}{7+2\sqrt{3}}=7-2\sqrt{3}\)
c:\(=\dfrac{\sqrt{5}\left(2\sqrt{2}-\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}-\sqrt{5}\right)}=\sqrt{\dfrac{5}{2}}=\dfrac{\sqrt{10}}{2}\)
d: \(=\dfrac{\left(1+\sqrt{a}\right)\cdot\left(2+\sqrt{a}\right)}{4-a}\)

a: \(=\sqrt{\left(2-a\right)^2\cdot\dfrac{2a}{a-2}}=\sqrt{2a\left(a-2\right)}\)
b: \(=\sqrt{\left(x-5\right)^2\cdot\dfrac{x}{\left(5-x\right)\left(5+x\right)}}\)
\(=\sqrt{\left(x-5\right)\cdot\dfrac{x}{x+5}}\)
c: \(=\sqrt{\left(a-b\right)^2\cdot\dfrac{3a}{\left(b-a\right)\left(b+a\right)}}=\sqrt{\dfrac{3a\left(b-a\right)}{b+a}}\)

bài 1 :
Hình : 2,43 2,43 0,9 A B C H
ta có : \(sin\widehat{BAH}=\dfrac{0,9}{2,43}=\dfrac{10}{27}\Rightarrow\widehat{BAH}\simeq21^o44'\)
\(\Rightarrow\widehat{ABC}=180^o-2\left(21^o44'\right)=136^o32'\)
vậy .....................................................................................................................
bài 2 : \(\dfrac{4}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}=\dfrac{4\left(1-\sqrt{\sqrt{5}-2}\right)}{\left(3+\sqrt{5}+\sqrt{2+2\sqrt{5}}\right)\left(1-\sqrt{\sqrt{5}-2}\right)}\)
\(=\dfrac{4\left(1-\sqrt{\sqrt{5}-2}\right)}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}-3\sqrt{\sqrt{5}-2}-\sqrt{5}\sqrt{\sqrt{5}-2}-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{4\left(1-\sqrt{\sqrt{5}-2}\right)}{4+\sqrt{2+2\sqrt{5}}-\left(3+\sqrt{5}\right)\sqrt{\sqrt{5}-2}}\) \(=\dfrac{4\left(1-\sqrt{\sqrt{5}-2}\right)}{4+\sqrt{2+2\sqrt{5}}-\sqrt{\left(\sqrt{5}-2\right)\left(14+6\sqrt{5}\right)}}\)\(=\dfrac{4\left(1-\sqrt{\sqrt{5}-2}\right)}{5}=1-\sqrt{\sqrt{5}-2}\)
bài 3 : 1) ta có : \(A=x+3\sqrt{x}-3=x+3\sqrt{x}+\dfrac{9}{4}-\dfrac{21}{4}\)
\(=\left(\sqrt{x}+\dfrac{3}{2}\right)^2-\dfrac{21}{4}\ge\left(\dfrac{3}{2}\right)^2-\dfrac{21}{4}\ge-3\)
dâu "=" xảy ra khi \(x=0\)
2) ta có : \(A=-2x-3\sqrt{x}+2=-2\left(x+\dfrac{3}{2}\sqrt{x}\right)+2\le2\)
dâu "=" xảy ra khi \(x=0\)
3) ta có : \(A=-4x-5\sqrt{x}-3=-4\left(x+\dfrac{5}{4}\sqrt{x}\right)-3\le-3\)
dâu "=" xảy ra khi \(x=0\)

bài 1) a) \(xy\sqrt{\dfrac{x}{y}}=x\sqrt{y}\sqrt{y}\dfrac{\sqrt{x}}{\sqrt{y}}=x\sqrt{x}\sqrt{y}=\left(\sqrt{x}\right)^3\sqrt{y}\)
b) \(\sqrt{\dfrac{5a^3}{49b}}=\dfrac{\sqrt{5a^3}}{\sqrt{49b}}=\dfrac{\sqrt{5a^3}}{7\sqrt{b}}=\dfrac{\sqrt{5a^3}.\sqrt{b}}{7\sqrt{b}.\sqrt{b}}=\dfrac{\sqrt{5a^3b}}{7b}\)
bài 2) a) \(\dfrac{\sqrt{3}-3}{1-\sqrt{3}}=\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}=\sqrt{3}\)
b) \(\dfrac{5-\sqrt{15}}{\sqrt{3}-\sqrt{5}}=\dfrac{-\sqrt{5}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}-\sqrt{5}}=-\sqrt{5}\)
c) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)

Em thử nhá, ko chắc đâu
1) \(\frac{2}{\sqrt{20}}=\frac{2\sqrt{20}}{20}\) 2) \(\frac{4}{\sqrt{8}}=\frac{4\sqrt{8}}{8}\)
3) \(\frac{2+\sqrt{3}}{\sqrt{2}}=\frac{2\sqrt{2}+\sqrt{6}}{2}\) 4) \(\frac{1}{\sqrt{6}-2}=\frac{\sqrt{6}+2}{6-4}=\frac{\sqrt{6}+2}{2}\)
5) \(\frac{1}{\sqrt{2}-\sqrt{3}}=\frac{\sqrt{2}+\sqrt{3}}{\left(\sqrt{2}-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{3}\right)}=-\left(\sqrt{2}+\sqrt{3}\right)\)
6) \(\frac{9a-b}{3\sqrt{a}-\sqrt{b}}=\frac{\left(9a-b\right)\left(3\sqrt{a}+b\right)}{\left(3\sqrt{a}-\sqrt{b}\right)\left(3\sqrt{a}+\sqrt{b}\right)}=\left(3\sqrt{a}+b\right)\)
7) + 8) em chưa nghĩ ra
ong tth :v
\(\frac{2}{\sqrt{20}}=\frac{\sqrt{4}}{\sqrt{4}.\sqrt{5}}=\frac{1}{\sqrt{5}}\)
\(\frac{4}{\sqrt{8}}=\frac{\sqrt{16}}{\sqrt{8}}=\sqrt{2}\)
\(\frac{2+\sqrt{3}}{\sqrt{2}}=\sqrt{2}+\frac{\sqrt{3}}{\sqrt{2}}=\sqrt{2}+\sqrt{1,5}\)
\(\frac{1}{\sqrt{6}-2}=\frac{\sqrt{6}+2}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}=\frac{\sqrt{6}+2}{2}\)
\(\frac{1}{\sqrt{2}-\sqrt{3}}=\frac{\sqrt{3}+\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{2}-\sqrt{3}\right)}=\frac{\sqrt{3}+\sqrt{2}}{-1}=-\sqrt{3}-\sqrt{2}\)
7: chưa
8: chưa
9:\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(\sqrt{2}+\sqrt{3}+2\right)+\left(2+\sqrt{6}+\sqrt{8}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\left(\sqrt{4}+\sqrt{6}+\sqrt{8}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(1+\sqrt{2}\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=1+\sqrt{2}\)

\(1a.\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\sqrt{7}+\sqrt{84}=21-2\sqrt{21}+2\sqrt{21}=21\) \(b.\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}=11+2\sqrt{30}-2\sqrt{30}=11\)
\(2a.\sqrt{\dfrac{a}{b}}+\sqrt{ab}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}.b^2}+\sqrt{\dfrac{a^2}{b^2}.\dfrac{b}{a}}=\sqrt{\dfrac{a}{b}}+b\sqrt{\dfrac{a}{b}}+\sqrt{\dfrac{a}{b}}=\left(2+b\right)\sqrt{\dfrac{a}{b}}\) \(b.\sqrt{\dfrac{m}{1-2x+x^2}}.\sqrt{\dfrac{4m-8mx+4mx^2}{81}}=\sqrt{\dfrac{m}{\left(x-1\right)^2}}.\sqrt{\dfrac{\left(2\sqrt{m}x-2\sqrt{m}\right)^2}{81}}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{\text{|}2\sqrt{m}x-2\sqrt{m}\text{|}}{9}=\dfrac{\sqrt{m}}{\text{|}x-1\text{|}}.\dfrac{2\sqrt{m}\text{|}x-1\text{|}}{9}=\dfrac{2m}{9}\) \(3a.VP=\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(\dfrac{1}{\sqrt{a}+1}\right)^2=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1=VT\)
KL : Vậy đẳng thức được chứng minh.
\(b.VP=\dfrac{a+b}{b^2}.\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{\text{|}a+b\text{|}}=\dfrac{a+b}{b^2}.\dfrac{b^2\text{|}a\text{|}}{a+b}=\text{|}a\text{|}=VT\)
KL : Vậy đẳng thức được chứng minh .
P/s : Dài v ~