Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bề rộng quang phổ liên tục bậc 3 là
\(L = x_{đỏ}^k-x_{ tím}^k= 3\frac{D}{a}(\lambda_d-\lambda_t)=2,85mm.\)
Với \(D = 2m; a= 0,8mm; \lambda_d = 0,76 \mu m; \lambda_t = 0,38 \mu m.\)

Vùng phủ nhau giữa quang phổ bậc 2 và bậc 3 là vùng quang phổ trải từ bậc 3 màu tím tới bậc 2 màu đỏ
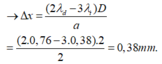
Đáp án C

Vùng phủ nhau giữa quang phổ bậc 2 và bậc 3 là vùng quang phổ trải từ bậc 3 màu tím tới bậc 2 màu đỏ
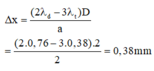
Đáp án A

Khoảng vân tím và khoảng vân đỏ :
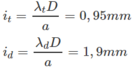
Bề rộng của quang phổ liên tục bậc 1 :
L 1 = i đ - i t = 1,9 - 0,95 = 0,95 mm Bề rộng của quang phổ liên tục bậc 3 :
L 3 = 3 i đ - 3 i t = 3.1,9 - 3.0,95 = 2,85 mm

\( i = \frac{\lambda D}{a}= 0,64 mm.\)
Số vân tối quan sát được trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=2.9=18.\)

Tại điểm M là vân sáng nên \(x_M=ki=k\frac{\lambda D}{a}\)
\(\lambda=\frac{x_Ma}{kD}=\frac{4,2.0,5}{k.1,4}=\frac{1,5}{k}\)
Theo giả thiết: \(0,38\le\lambda\le0,76\)
\(\Rightarrow0,38\le\frac{1,5}{k}\le0,76\)
\(\Rightarrow1,97\le k\le3,94\)
k nguyên nên k = 2,3.
Như vậy, tại M có 2 bước sóng cho vân sáng, đáp án là A.



Đáp án D
+ Vùng phủ nhau giữa quang phổ bậc 3 và bậc 4: