Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Khoảng vân: ![]()
Số vân sáng, tối quan sát được trên trường giao thoa:
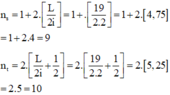




Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 2 - II.6. Ứng dụng xác định quãng đường vật đi được trong khoảng thời gian ∆t bất kỳ Phần 1 - Luyện thi THPTQG môn Vật Lý - Thầy Lê Xuân Vượng - Nền tảng 8+
Video không hỗ trỡ trên thiết bị của bạn!
IV. CÁC DẠNG BÀI TOÁN ĐẠI CƯƠNG VỀ DÒNG XOAY CHIỀU - Dạng 1 - Luyện thi THPTQG môn Vật Lý - Thầy Lê Xuân Vượng - Nền tảng 8+
Video không hỗ trỡ trên thiết bị của bạn!
Bài 3 – Con lắc lò xo - Thời gian lò xo bị nén, giãn trong một chu kỳ Phần 2 - Luyện thi THPTQG môn Vật Lý - Thầy Lê Xuân Vượng - Nền tảng 8+
Video không hỗ trỡ trên thiết bị của bạn!
Bài 13: Dao động điện từ - Các dạng bài tập đặc trưng của mạch LC Dạng 5 - Luyện thi THPTQG môn Vật Lý - Thầy Lê Xuân Vượng - Nền tảng 8+
Video không hỗ trỡ trên thiết bị của bạn!
Bài học: Bài toán xác định quãng đường, quãng đường lớn nhất nhỏ nhất (Phần 3) - Luyện thi THPTQG môn Lý - Thầy Kim Nhật Trung - MỤC TIÊU 8+

Đáp án A.
- Tại vị trí hai vân sáng trùng nhau:
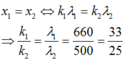
- Vân sáng gần nhất ứng với các số nguyên
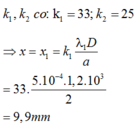


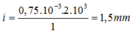


Đáp án D
- Số vân sáng trên trường giao thoa:
+ Số vân sáng: N S = 1 + 2. L 2 i Chia lấy phần nguyên
+ Số vân tối: N T = 2. L 2 i + 0 , 5 Chia lấy phần nguyên
- Áp dụng ta có:
+ Khoảng vân i = λ D a = 0 , 6.2 , 5 1 = 1 , 5 m m
+ Số vân sáng: N S = 1 + 2. L 2 i = 9
+ Số vân tối: N T = 2. L 2 i + 0 , 5 = 10
- Vậy tổng số vân sáng và tối trong miền giao thoa là 19 vân