Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: sử dụng công thức vân sáng
Cách giải:
Tại M là vân sáng bậc 9, bậc k, bậc 2 k nên có:
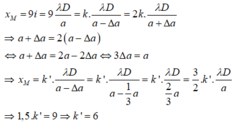
Đáp án B

Ta có:
\(i=\frac{D\text{λ}}{a}\)
Điểm M cách vân trung tâm một đoạn l thì
\(l=4i=4\frac{D\text{λ}}{a}\)
Từ đó ta suy ra được
\(\frac{4}{a}=\frac{k}{a-\text{Δa}}=\frac{3k}{a+\text{Δa}}=\frac{4k}{a-\text{Δa}+a+\text{Δa}}\)\(=\frac{4k}{2a}=\frac{2k}{a}\)
k=2
\(4\left(a-\text{Δa}\right)=ka=2a\) suy ra \(\text{Δa}=\frac{a}{2}\)
Khi tăng khoảng cách khe lên
\(\frac{4}{a}=\frac{k'}{a+2\text{Δa}}\)
\(k'=8\)
----> chọn C

Chọn A
Khi giảm đi 1 lượng Δa thì tại M là vân bậc k tức là:
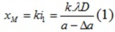
Khi tăng thêm 1 lượng Δa thì tại M là vân bậc k tức là:
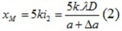
Từ (1) và (2) => a = 3Δa/2
=> Nếu tăng thêm khoảng cách S1S2 thêm 3Δa thì khoảng vân mới là:
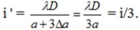
Lại có ban đầu M là vân sáng bậc 3 => xM = 3i => xM = 9i'
=> Sau khi tăng khoảng cách S1S2 thêm 3Δa thì tại M là vân sáng bậc 9

Chọn C
Khi giảm đi 1 lượng Δa thì tại M là vân bậc k tức là:
![]()
Khi tăng thêm 1 lượng Δa thì tại M là vân bậc k tức là:
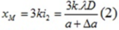
Từ (1) và (2) => a = 2Δa
=> Nếu tăng thêm khoảng cách S1S2 thêm 2Δa thì khoảng vân mới là:
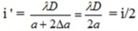
Lại có ban đầu M là vân sáng bậc 4 => xM = 4i => xM = 8i'
=> Sau khi tăng khoảng cách S1S2 thêm 2Δa thì tại M là vân sáng bậc 8

Chọn A
Khi giảm đi một lượng Δa thì tại M là vân bậc k tức là:
![]()
Khi tăng thêm 1 lượng Δa thì tại M là vân bậc k tức là:
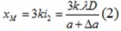
Từ (1) và (2) => a = 2Δa
=> Nếu tăng thêm khoảng cách S1S2 thêm 2Δa thì khoảng vân mới là:
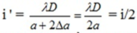
Lại có ban đầu M là vân tối thứ tư => xM = 3,5i => xM = 7i'
Sau khi tăng khoảng cách S1S2 lên 2Δa thì tại M là vân sáng bậc 7

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

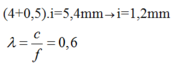
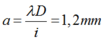
Chọn A.
Tại đó vân sáng bậc k nên: d 2 − d 1 = k λ = k c f .