Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

Khi \(S_1S_2=a\) tại M là vân sáng bậc 4 nên \(x_M=4i_1.\)
Nếu tăng S1S2 một lượng \(\Delta a\) thì khoảng vân giảm => M là vân sáng bậc 3k.
tức là \(x_M=3ki_2.\left(2\right)\)
Nếu giảm S1S2 một lượng \(\Delta a\) thì khoảng vân tăng => M là vân sáng bậc k
tức là \(x_M=ki_3.\left(3\right)\)
Cho (2) = (1) => \(\frac{i_1}{i_2}=\frac{a+\Delta a}{a}=\frac{4}{k}=.\left(3\right)\)
Cho (3) = (1) => \(\frac{i_1}{i_2}=\frac{a-\Delta a}{a}=\frac{4}{3k}.\left(4\right)\)
Chia (3) cho (4) ta được:
\(\frac{\left(a+\Delta a\right)}{\left(a-\Delta a\right)}=3\Rightarrow\Delta a=0.5a\)
Nếu tăng a thêm 2\(\Delta a\)=> \(x_M=ki_4=\frac{k\lambda D}{a+2\Delta a}=\frac{k\lambda D}{2a}=\frac{k}{2}i_1\)
So sánh với (1)=> \(\frac{k}{2}=4\Rightarrow k=8\)
Như vậy M là vân sáng bậc 8.

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Đáp án D
+ Khi khoảng cách 2 khe tới màn là a thì tại M là vân sáng bậc 4 nên



Đáp án D
+ Khi khoảng cách 2 khe tới màn là a thì tại M là vân sáng bậc 4 nên



Ta có: \(i_1=3,5/7=0,5mm\)
\(i_2=7,2/8=0,9mm\)
Vân sáng: \(i=\dfrac{\lambda D}{a}\)
Suy ra: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow \lambda_2=\lambda_1.\dfrac{i_2}{i_1}=420.\dfrac{0,9}{0,5}=756nm\)
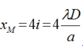
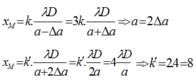

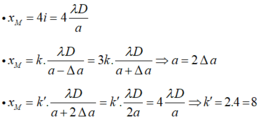
Phương pháp:
sử dụng công thức tính khoảng vân và vị trí vân sáng
Cách giải:
Áp dụng công thức tính vị trí vân sáng:
Vậy M trở thành vân sáng bậc 8
Đáp án A