Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
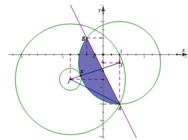
Do 
nên tập hợp điểm M là các điểm nằm ngoài đường tròn 
và nằm trong đường tròn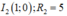 
Dựa vào hình vẽ ta chứng minh được 
Khi đó 
Lời giải:
Đặt \(z=a+bi\)
Ta có: \(|z|-2\overline{z}=-7+3i+z\)
\(\Leftrightarrow \sqrt{a^2+b^2}-2(a-bi)=-7+3i+a+bi\)
\(\Leftrightarrow (\sqrt{a^2+b^2}-2a)+2bi=(-7+a)+i(b+3)\)
\(\Rightarrow \left\{\begin{matrix} \sqrt{a^2+b^2}-2a=-7+a(1)\\ 2b=b+3(2)\end{matrix}\right.\)
Từ (2) suy ra \(b=3\)
Thay vào (1): \(\sqrt{a^2+9}=3a-7\)
\(\Rightarrow (3a-7)^2=a^2+9\)
\(\Leftrightarrow 9a^2+49-42a=a^2+9\)
\(\Leftrightarrow 8a^2-42a+40=0\)
\(\Leftrightarrow a=4\) (chọn) hoặc \(a=\frac{5}{4}\) (loại do \(a\in\mathbb{Z}\) )
Vậy số phức \(z=4+3i\)
\(\Rightarrow w=1-(4+3i)+(4+3i)^2=4+21i\)
\(\Rightarrow |w|=\sqrt{4^2+21^2}=\sqrt{457}\)
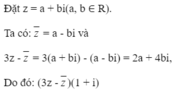
= 2a - 4b + (2a + 4b)i - 5(a + bi) = 8i - 1
Theo giả thiết: (2a - 4b) + (2a + 4b)i - 5(a + bi) = 8i - 1
⇔ -3a - 4b + (2a - b)i = -1 + 8i
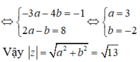
Chọn C
Đặt z = a + bi(a, b ∈ R). Ta có
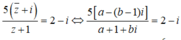
⇔ 5a - 5(b - 1)i = (2 - i)(a + 1 + bi)
⇔ 3a - b - 2 + (a - 7b + 6)i = 0
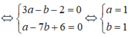
Suy ra z = 1 + i và w = 1 + ( 1 + i ) + ( 1 + i ) 2 = 2 + 3 i .
Vậy: | w | = ( 4 + 9 ) = 13
Chọn B
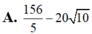
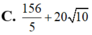
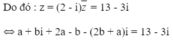
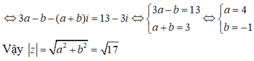
Đáp án D
Cách giải: gọi z=x+yi
Vậy quỹ tích các điểm z thuộc đường tròn tâm I(4;-3); R=3
Đặt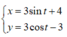
(theo bunhiacopxki)