Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
![]()
Xác suất cần tìm:
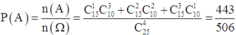

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
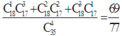

Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
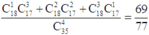

số cách gọi 4 hs lên bảng là: \(C^4_{25}\)Gọi A là biến cố :" bốn hs lên bảng có cả nam và nữ:
=> ta phải tính n(A)=?
phương án 1; 3 nam và 1 nữ: \(C^3_{15}.C^1_{10}=4550\)
phương án 2: 2 nam và 2 nữ : \(C^1_{15}.C^2_{10}=4725\)
phương án 3: 1 nam vfa 3 nữ: \(C^1_{15}.C^3_{10}=1800\)
=> n(A)=4550+4725+1800=11075 cách
=> p(A)=\(\frac{11075}{C^4_{25}}=\frac{443}{506}\)
chue yếu bạn áp dụng các quy tắc cộng và nhân là xong

Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là 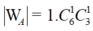 .
.
Vậy xác suất cần tính 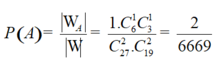 .
.
Chon C.

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 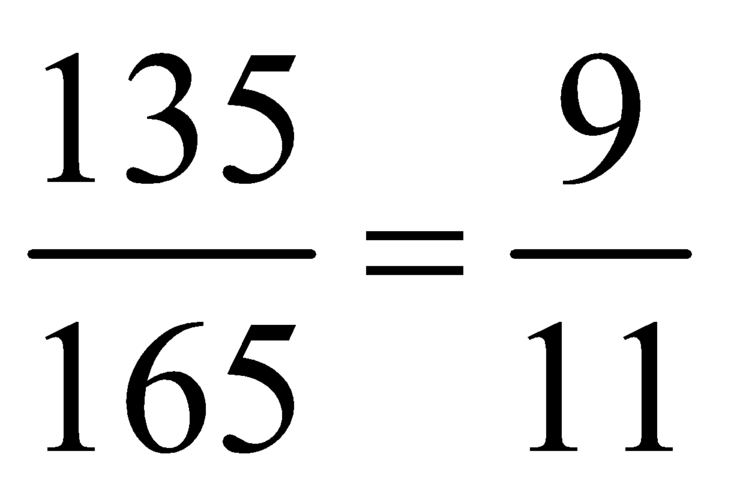 .
.

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
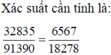

Đáp án C.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 3 học sinh trong 10 học sinh có C 10 3 cách => n ( Ω ) = C 10 3 = 120 .
Gọi X là biến cố trong 3 học sinh được chọn có ít nhất một học sinh nữ
Ta xét các trường hợp sau:
TH1. Chọn 1 học sinh nữ và 2 học sinh nam => có C 7 2 . C 3 1 = 63 cách.
TH2. Chọn 2 học sinh nữ và 1 học sinh nam => có C 7 1 . C 3 2 = 21 cách.
TH3. Chọn 3 học sinh nữ và 0 học sinh nam => có C 3 3 = 1 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 63 + 21 + 1 = 85.
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 85 120 = 17 24 .

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là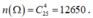
Ta có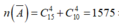
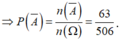
Vậy xác suất của biến cố A là