Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Mỗi vé số gồm 6 kí tự nên số phần tử không gian mẫu là ![]()
Gọi A là biến cố An trúng được giải đặc biệt. Ta có ![]()
Vậy xác suất để An trúng được giải đặc biệt là ![]()

Đáp án C.
Không gian mẫu: ![]()
Gọi biến cố A là: “Người đó không trúng vé nào”
![]()
Xác suất của biến cố A là ![]()

Đáp án A
Mua 15 vé trong 100 vé có C 15 3 cách => n ( Ω ) = C 15 3 .
Gọi X là biến cố “người đó trúng 2 vé”
Mua 2 vé trúng trong 5 vé trúng có C 5 2 cách, mua 13 vé còn lại trong 95 vé có C 95 13 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n ( X ) = C 5 2 . C 95 13
Vậy xác suất cần tính P = n ( X ) n ( Ω ) = C 5 2 . C 95 13 C 100 15 ≈ 14 % .

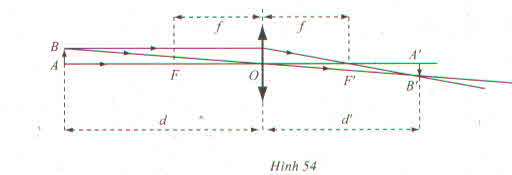
a) Từ hệ thức suy ra d' = φ(d) =
.
b) +) φ(d) =
= +∞ .
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.
+) φ(d) =
= -∞.
Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.
+) φ(d) =
=
= f.
Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

Câu 1:
Khong gian mẫu: \(C_{11}^3\)
Có 5 cặp bi cùng số, do đó có \(5\) cách chọn ra 1 cặp cùng số, viên còn lại có 9 cách chọn \(\Rightarrow\) có 45 cách chọn 3 viên có 2 viên cùng số (tất nhiên là ko thể 3 viên cùng số được)
Xác suất: \(P=\frac{C_{11}^3-45}{C_{11}^3}=\frac{8}{11}\)
Câu 2:
Không gian mẫu: \(9!\)
Xếp 4 bạn nam cạnh nhau và hoán vị, có \(4!\) cách
Coi 4 bạn nam này là 1 người, xếp hàng cùng 5 bạn nữ \(\Rightarrow\) có \(6!\) cách hoán vị
Vậy có \(4!.6!\) cách
Xác suất: \(P=\frac{4!.6!}{9!}=\frac{1}{21}\)

1/
Bạn chỉ cần tìm sin, cos trong \(\left[0;2\pi\right]\) là đủ (vì cả 2 hàm đều tuần hoàn với chu kì \(2\pi\))
Đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\) với \(a\in\left[0;2\pi\right]\)
\(\Rightarrow4sina.cosa\left(2cos^2a-1\right)=1\)
\(\Leftrightarrow2sin2a.cos2a=1\Leftrightarrow sin4a=1\)
\(\Rightarrow4a=\frac{\pi}{2}+k2\pi\Rightarrow a=\frac{\pi}{8}+\frac{k\pi}{2}\)
\(\Rightarrow0\le\frac{\pi}{8}+\frac{k\pi}{2}\le2\pi\Rightarrow a=\left\{\frac{\pi}{8};\frac{5\pi}{8};\frac{9\pi}{8};\frac{13\pi}{8};\frac{17\pi}{8}\right\}\)
\(\Rightarrow\left(x;y\right)=\left(sin\frac{\pi}{8};cos\frac{\pi}{8}\right);\left(sin\frac{5\pi}{8};cos\frac{5\pi}{8}\right)...\)
2.
\(sinx=\frac{1}{3}\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+l2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)\\x=\pi-arcsin\left(\frac{1}{3}\right)\end{matrix}\right.\)
(Vì \(0< \frac{1}{3}< 1\) nên \(0< arcsin\left(\frac{1}{3}\right)< \frac{\pi}{2}\) do đó nếu \(k>0\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi>2\pi\) ; nếu \(k\le-1\Rightarrow arcsin\left(\frac{1}{3}\right)+k2\pi\le-\frac{3\pi}{2}\) đều ko thuộc \(\left[0;\pi\right]\Rightarrow k=0\).
Tương tự với \(l\))
Cho mình hỏi sao từ 0 < 1/3 < 1 thì suy ra đc 0 < arcsin (1/3) < pi/2 vậy?

Nếu người giữ vé số 47 trúng một trong bốn giải thì:
Người giữ vé số 47 có 4 cách chọn giải.
Ba giải còn lại ứng với một chỉnh hợp chấp 3 của 99 phần tử, do đó ta có A 99 3 = 941094 cách .
Vậy số kết quả bằng 4 × A 99 3 = 4 × 941094 = 3764376 kết quả.
Chọn đáp án D.