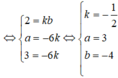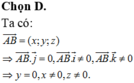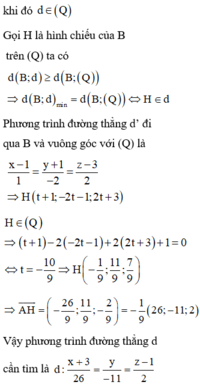Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b
Đáp án D
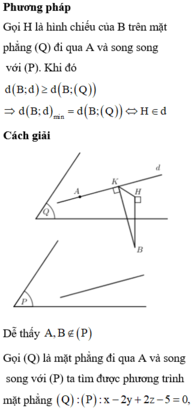
Phương pháp :
Đường thẳng qua A song song với hai mặt phẳng (P); (Q) nhận 
là 1VTCP.
Cách giải : Ta có 
lần lượt là các VTPT của
Ta có :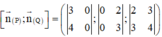
là 1 VTCP của đường thẳng qua A và vuông góc với cả
Vậy phương trình đường thẳng cần tìm là: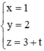 
Với t = -3 ta có đường thẳng đi qua điểm B(1;2;0) => phương trình đường thẳng cần tìm là :
x = 1 y = 2 z = t
ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b
Đáp án C
Gọi (Q) là mặt phẳng qua A và song song với
P ⇒ Q : x + y + 2 z − 4 = 0
Ta có d B ; d ≤ A B ⇒ d B , d max ⇔ AB ⊥ d.
Ta có A B ¯ = 1 ; − 1 ; 0 ⇒ u d ¯ = A B ¯ , n p ¯ = − 2 ; − 2 ; 2
Do đó phương trình đường thẳng d là d : x − 2 1 = y − 2 1 = z − 1 .
Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
