Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có : \(\overrightarrow{AB}=\left(-a;b;0\right)\)
và \(\overrightarrow{AC}=\left(-a;0;c\right)\)
Vì \(\overrightarrow{AB}.\overrightarrow{AC}=a^2>0\) nên góc \(\widehat{BAC}\) là góc nhọn
Lập luận tương tự chứng minh được các góc \(\widehat{B}\) và \(\widehat{C}\) cũng là góc nhọn
C K O E H F B A D
Trên \(\Delta\) lấy điểm D sao cho à D, A nằm khác phía nhau so với B. Gọi E là giao điểm của các đường thẳng KA và OC; Gọi F là giao điểm của các đường thẳng KB và OD
Vì K là tâm đường tròn bàng tiếp góc O của tam giác OAB nên KE là phân giác của góc OAC. Mà OAC là tam giác cân tại A ( do OA = AC, theo gt) nên suy ra KE cũng là đường trung trục của OC. Do đó, E là trung điểm của OC và KC=KO
Xét tương tự đối với KF, ta cũng có F là trung điểm của OD và KD=KO
Suy ra tam giác CKD cân tại K. Do đó, hạ KH vuông góc với \(\Delta\) , ta có H là trung điểm của CD. Như vậy :
+ A là giao của \(\Delta\) và đường trung trực \(d_1\) của đoạn OC (1)
+ B là giao của \(\Delta\) và đường trung trực \(d_2\) của đoạn OD, với D là điểm đối xứng của C qua H là hình chiếu vuông góc của K trên \(\Delta\) (2)
Vì \(C\in\Delta\) và có hoành độ \(x_0=\frac{24}{5}\) nên gọi \(y_0\) là tung độ của C, ta có :
\(2.\frac{24}{5}+3y_0-12=0\) suy ra \(y_0=-\frac{12}{5}\)
Từ đó, trung điểm E của OC có tọa độ là \(\left(\frac{12}{5};-\frac{6}{5}\right)\) và đường thẳng OC có phương trình \(x+2y=0\)
Suy ra phương trình của \(d_1\) là \(2x-y-6=0\)
Do đó, theo (1), tọa độ của A là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\2x-y-6=0\end{cases}\)
Giải hệ ta có \(A=\left(3;0\right)\)
Để tìm tọa độ đỉnh B ta làm như sau :
Gọi d là đường thẳng đi qua K(6;6) và vuông góc với \(\Delta\).
Ta có phương trình của d là : \(3x-4y+6=0\). Từ đây, do H là giao điểm của \(\Delta\). và d nên tọa độ của H là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\3x-4y+6=0\end{cases}\)
Giải hệ trên, ta được \(H=\left(\frac{6}{5};\frac{12}{5}\right)\) suy ta \(D=\left(-\frac{12}{5};\frac{26}{5}\right)\)
Do đó, trung điểm F của OD có tọa độ là \(\left(-\frac{6}{5};\frac{18}{5}\right)\) và đường thẳng OD có phương trình \(3x+y=0\)
Suy ra phương trình của \(d_2\) là \(x-3y+12=0\)
Do đó, theo (2), tọa độ B là nghiệm của hệ phương trình :
\(\begin{cases}4x+3y-12=0\\x-3y+12=0\end{cases}\)
Giải hệ trên ta được B=(0;4)
Chọn A.
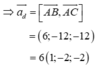
Đường thẳng d đi qua G(2;-1;0) và có vectơ chỉ phương là 
Vậy phương trình tham số của d là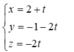 
Chọn C
Do tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc và H là trực tâm tam giác ABC nên 
Phương trình mặt phẳng (ABC) là 
hay 6x + 4y + 3z - 12 = 0
Vì 
nên đường thẳng OH có véc-tơ chỉ phương 
Mà đường thẳng OH đi qua O nên phương trình tham số của đường thẳng OH là: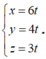 
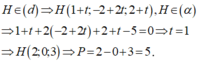
Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.