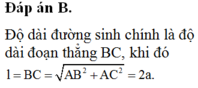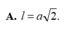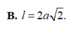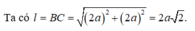Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Xét tam giác \(PBC\)và tam giác \(PAB\)có:
\(\frac{PB}{PA}=\frac{BC}{AB}=\frac{PC}{PB}=\sqrt{2}\)
suy ra \(\Delta PBC~\Delta PAB\left(c.c.c\right)\)
suy ra \(\widehat{PBC}=\widehat{PAB}\).
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}\)
\(=180^o-45^o-135^o\)

Chọn A.
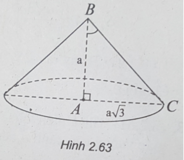
(h.2.63) Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.
Theo định lý Py-ta-go, ta có:
BC 2 = AB 2 + AC 2 = a 2 + 3 a 2 = 4 a 2
⇒ BC = 2a.
Vậy độ dài đường sinh của hình nón là l = 2a.

9.
\(R=\frac{AB}{2}=\frac{a}{2}\) ; \(l=AB=a\)
\(h=\sqrt{l^2-R^2}=\frac{a\sqrt{3}}{2}\)
Thể tích chóp:
\(V=\frac{1}{3}\pi R^2h=\frac{\sqrt{3}}{6}\pi a^3\)
10.
Gọi thiết diện là tam giác ABC vuông cân tại A
\(BC=a\Rightarrow R=\frac{BC}{2}=\frac{a}{2}\)
\(l=AB=\frac{BC}{\sqrt{2}}=\frac{a\sqrt{2}}{2}\)
\(S_{xq}=\pi Rl=\frac{\sqrt{2}}{4}\pi a^2\)
6.
\(l=BC=\sqrt{AB^2+AC^2}=2a\)
7.
\(h=AC=\frac{AB}{tan30^0}=a\sqrt{3}\) ; \(R=AB=a\)
\(V=\frac{1}{3}\pi R^2h=\frac{\sqrt{3}}{3}\pi a^3\)
8.
Gọi O là tâm đáy
\(\Rightarrow R=OB=\frac{2}{3}.\frac{BC\sqrt{3}}{2}=\frac{BC\sqrt{3}}{3}=a\sqrt{3}\)
\(l=AB=3a\)
\(S_{xq}=\pi Rl=3\sqrt{3}\pi a^2\)

Chọn C.

Độ dài đường sinh l bằng độ dài cạnh BC của tam giác vuông ABC.
Theo định lý Pytago thì:
BC2 = AB2 + AC2 = a2 + 3a2 = 4a2 ⇒ BC = 2a
Vậy độ dài đường sinh của hình nón là l = 2a.

Bài 14:
Vecto chỉ phương của đường thẳng $d$ là: $\overrightarrow{u_d}=(1; -1; 2)$
Mp $(P)$ vuông góc với $d$ nên nhận $\overrightarrow{u_d}$ là vecto pháp tuyến
Do đó PTMP $(P)$ là:
$1(x-x_M)-1(y-y_M)+2(z-z_M)=0$
$\Leftrightarrow x-y+2z=0$
Đáp án A
Bài 13:
Khi quay tam giác đều ABC quanh cạnh AB thì ta thu được một khối hình là hợp của 2 hình nón (ngược chiều nhau) có cùng bán kính đáy $r$ là đường cao của tam giác đều, tức là $r=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$ và đường cao là $h=\frac{AB}{2}=\frac{1}{2}$
Thể tích 1 hình nón: $V_n=\frac{1}{3}\pi r^2h=\frac{\pi}{8}$
Do đó thể tích của khối hình khi quay tam giác đều ABC quanh AB là: $2V_n=\frac{\pi}{4}$