Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
(1) Sai vì ( α ) // a ( β ) // a ( α ) ∩ ( β ) = d ⇒ a / / d tức là có trường hợp chúng cắt nhau.

Đáp án D
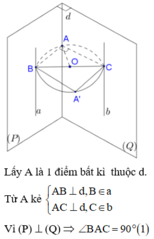
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4:
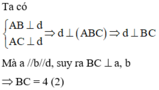
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2

a) Ta có: góc FAB + góc BAC = 90 độ
góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC
b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM
c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.

Đáp án C
Mệnh đề 1 đúng.
Mệnh đề 2 sai vì 2 đường thẳng đó có thể chéo nhau.
Mệnh đề 3 sai vì 2 đường thẳng đó có thể song song.
Mệnh đề 4 sai

Chọn C.
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Đáp án C
Trong không gian a và b có thể cắt nhau và cùng thuộc mặt phẳng song song với mặt phẳng đã cho.


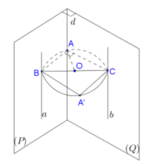
Hình ảnh minh họa hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R) nhưng không song song với nhau