Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Bước sóng λ = v/f = 1,5 cm
Số điểm dao động với biên độ cực đại trên AB là số giá trị nguyên của k thỏa mãn
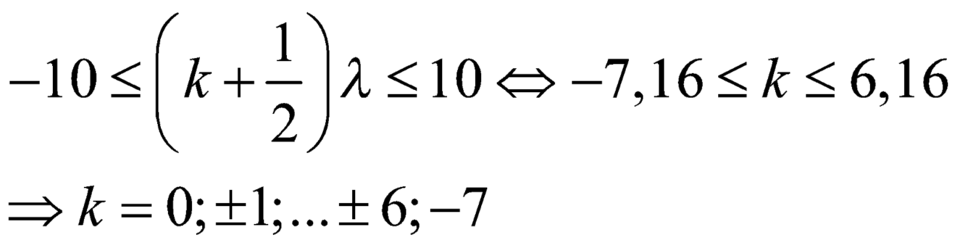
![]() Có 14 điểm
Có 14 điểm

Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG

a)\(U_M=2Acos\left(\pi\frac{\left(d_2-d_1\right)}{\lambda}\right)\) \(cos\left(\omega t-\pi\frac{d_1+d_2}{\lambda}\right)\)
thay số vào ta đc
\(U_M=\frac{\sqrt{2}}{2}cós\left(20\pi t-\frac{29\pi}{4}\right)\)
b) số cực đại \(\frac{-AB}{\lambda}\le n\le\frac{AB}{\lambda}\)
nên \(-2,75\le n\le2,75\)
có 5 giá trị n nguyên, vậy số cực đại là 5
số cực tiểu \(\frac{-AB}{\lambda}-\frac{1}{2}\le n\le\frac{AB}{2}-\frac{1}{2}\)
thay số tương tự nhé
ừ thì bước sóng bằng 8cm đúng rồi
còn d2 với d1 thì k quan trọng đâu, lấy cái nào trừ cái nào cũng đc

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

\(\lambda =\frac{v}{f}=\frac{50}{10}=5cm.\)
Điểm M ngược pha với điểm I khi: \(\triangle \phi=\phi_I-\phi_M = 2\pi \frac{d_1-d_{1}^{'}}{\lambda}=(2k+1)\pi \Rightarrow d_1-d_1^{'}=(2k+1)\frac{\lambda}{2}\)
Để điểm M gần I nhất thì hiệu d1 - d1' cũng phải nhỏ nhất khi đó k chỉ nhận giá trị nhỏ nhất là k = 0.
\(d_{1}-d_{1}^{'}=(2.0+1)\frac{5}{2}=2.5cm\Rightarrow d_1 = 7.5cm.\)
\(\Rightarrow MI= \sqrt {d_1^{2}-d_1^{'2}}\) = \(\sqrt{7.5^2-2.5^2}=\sqrt{50}cm\)

Đáp án C
Bước sóng λ = v/f = 1,5 cm
Số điểm dao động với biên độ cực đại trên AB là số giá trị nguyên của k thỏa mãn
=> k: 0; ±1;…±6; - 7
=> Có 14 điểm