Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A.
• Ta tìm số cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn.
Có 3 trường hợp :
• 7 cuốn còn lại gồm 2 môn toán lý : có C 9 7 cách
• 7 cuốn còn lại gồm 2 môn lý hóa : có C 11 7 cách
• 7 cuốn còn lại gồm 2 môn toán hóa : có C 10 7 cách
Suy ra có C 9 7 + C 11 7 + C 10 7 = 486 cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn. Do đó số cách chọn 8 cuốn sao cho 7 cuốn còn lại có đủ 3 môn là C 15 7 − 486 = 5949 cách.
Xác suất cần tìm là P = 5949 C 15 7 = 661 715 .

Chọn A
Giả sử có a học sinh nhận sách Toán và Lí, b học sinh nhận sách Lí và Hóa, c học sinh nhận sách Toán và Hóa.
Suy ra
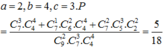

Đáp án A
Lấy quyển đầu tiên là Văn trong 9 quyển Văn có C 9 1 cách
Lấy quyển đầu tiên là Văn trong 8 quyển Văn có C 8 1 cách
Lấy quyển đầu tiên là Anh trong 6 quyển Anh có C 6 1 cách
Suy ra số kết quả thuận lợi của biến cố là n X = 9.8.6 = 432
Vậy xác suất cần tính là P = n X n Ω = 432 15.14.13 = 72 455

Đáp án D.
Sô cách lấy bằng số cách chọn ra 6 quyển để bỏ lại. Yêu cầu đặt ra là 6 quyển để lại phải đủ cả 3 môn.
TH1: 1 văn, 2 âm nhạc, 3 hội họa: C 5 1 . C 4 2 . C 3 3 .
TH2: 1 văn, 3 âm nhạc, 2 hội họa: C 5 1 . C 4 3 . C 3 2 .
TH3: 1 văn, 4 âm nhạc, 1 hội họa: C 5 1 . C 4 4 . C 3 1
TH4: 2 văn, 1 âm nhạc, 3 hội họa: C 5 2 . C 4 1 . C 3 3 .
TH5: 2 văn, 2 âm nhạc, 2 hội họa: C 5 2 . C 4 2 . C 3 2 .
TH6: 2 văn, 3 âm nhạc, 1 hội họa: C 5 2 . C 4 3 . C 3 1 .
TH7: 3 văn, 1 âm nhạc, 2 hội họa: C 5 3 . C 4 1 . C 3 2 .
TH8: 3 văn, 2 âm nhạc, 1 hội họa: C 5 3 . C 4 2 . C 3 1 .
TH9: 4 văn, 1 âm nhạc, 1 hội họa: C 5 4 . C 4 1 . C 3 1 .
Lấy 6 quyển sách chia cho 6 bạn: 6 ! = 720
Nhân lại ta có : 579600 cách

Đáp án A
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản trong bài toán sắp xếp đồ vật
Lời giải: Xếp 5 quyển Toán (coi Toán T1 và Toán T2 là một) có 5 ! .2 ! = 240 cách.
Khi đó, sẽ tạo ra 4 khoảng trống kí hiệu như sau: _T_T_T_T_T_
Xếp 3 quyển sách Tiếng Anh vào 4 khoảng trống giữa hai quyển toán có A 4 3 cách.
Xếp 1 quyển sách Văn vào 3 vị trí còn lại có 3 cách.
Vậy xác suất cần tính là P = 240. A 4 3 .3 10 ! = 1 210 .

HD: Xếp 10 quyển sách tham khảo thành một hàng ngang trên giá sách có : 10! cách sắp xếp.
Sắp xếp 2 cuốn toán 1 và toán 2 cạnh nhau có 2! cách,
Sắp xếp 6 cuốn sách Toán sao cho có hai quyển Toán T1 và Toàn T2 cạnh nhau có 2!.5! cách.
Khi đó có 4 vị trí để sắp xếp 3 cuốn Anh ở giữa hai quyển Toán và 3 cách sắp xếp cuốn Tiếng Anh.
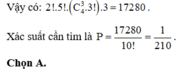

Gọi x là số trang của quyển sách
Số trang sách ngày thứ nhất đọc là \(\frac{1}{3}x\)
Số trang sách ngày thứ hai đọc là \(\frac{5}{8}\left(x-\frac{x}{3}\right)=\frac{5x}{12}\)
Theo đề bài ta có phương trình:
\(x-\frac{x}{3}-\frac{5x}{12}=90\)
<=> 12x-4x-5x=1080
<=> 3x=1080
<=> x=360(trang)
Vậy quyển sách có 360 trang

Chọn A.
Gọi a ; b ; c 1 ≤ a < b < c ≤ 20 tương ứng là vị trí của 3 cuốn sách được lấy. Để giữa 2 cuốn lấy được bất kì luôn có ít nhất 2 cuốn không được lấy thì điều kiện cần và đủ là b - a > 2 và c - a > 2 . Tức là 5 ≤ a + 4 < b + 2 < c ≤ 20 . Như vậy số cách lấy ra 3 cuốn sách thỏa mãn yêu cầu chính là số cách lấy ra 3 số nguyên dương trong 16 số( từ 5 đến 20 có tất cả 16 số) và bằng C 16 3 .
Chọn B.
Lần lượt lấy 3 cuốn mà không để lại vào kệ có: 15.14.13 cách lấy.
Gọi A là biến cố: “2 cuốn đầu là sách Toán và cuốn thứ 3 là sách Văn”
Ta có: Ω A = 10 . 9 . 5
Xác suất cần tìm là: P A = 15 91 .