Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

6 tháng 9 2019

Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

#Toán lớp 10

1

CM

Cao Minh Tâm

6 tháng 9 2019

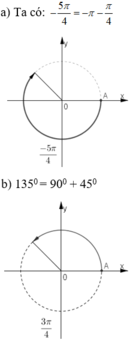
Giải bài 5 trang 140 SGK Đại Số 10 | Giải toán lớp 10

Giải bài 5 trang 140 SGK Đại Số 10 | Giải toán lớp 10

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

29 tháng 3 2017

Trên đường tròn lượng giác hãy biểu diễn các cung có số đo :

a) \(-\dfrac{5\pi}{4}\)

b) \(135^0\)

c) \(\dfrac{10\pi}{3}\)

d) \(-225^0\)

#Toán lớp 10

1

ND

Nguyễn Đắc Định

15 tháng 4 2017

a) Trên hình bên. Cung có số đo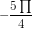

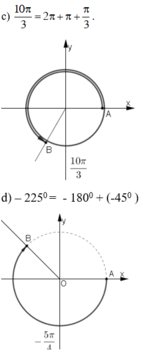
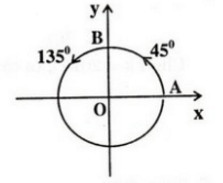
b) Nhận xét rằng 135⁰ – ( -225⁰ ) = 360⁰ . Như vậy cung 135⁰ và cung -225⁰ có chung điểm ngọn. Mà cung 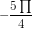cũng là cung -225⁰ . Vậy cung 135⁰ cũng chính là cung theo chiều dương

c)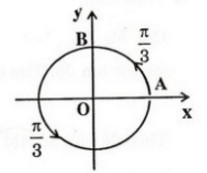

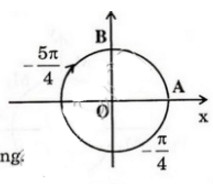
d)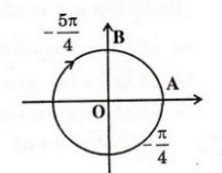

UN

Uyên Nguyễn

10 tháng 2 2017

các bạn ơi giải dùm mình câu này nhanh nhá!!!

#Toán lớp 10

0

NH

Nguyễn Hồ Đức Cường

16 tháng 10 2020 - olm

Giải các phương trình:

#Toán lớp 10

0

PT

Pham Trong Bach

25 tháng 9 2017

Khi biểu diễn trên đường tròn lượng giác các cung lượng giác nào trong các cung lượng giác có số đo dưới đây có cùng ngọn cung với cung lượng giác có số đo 42000 A.1300 B.1200 C.-1200 D.600...

#Toán lớp 10

1

CM

Cao Minh Tâm

25 tháng 9 2017

Chọn C.

Ta có 4200⁰ = - 120⁰ + 12. 360⁰

nên cung có số đo – 120⁰ có ngọn cung trùng với ngọn cung có số đo 4200⁰.

CX

Chiều Xuân

5 tháng 11 2017

đây nữa ạ:

#Toán lớp 10

0

TH

Thị Huế Nguyễn

17 tháng 3 2019 - olm

Cung lượng giác AD có số đo là bao nhiêu ?

#Toán lớp 10

0

CX

Chiều Xuân

5 tháng 11 2017

đây nữa ạ, giúp em với

#Toán lớp 10

0

CN

Cô Nàng Vui Vẻ

23 tháng 4 2016

Bài 1. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau: Bài 2. Cho a, b, c ³ 0. Chứng minh các bất đẳng thức sau:Bài 3. Cho a, b, c > 0. Chứng minh các bất đẳng thức...

#Toán lớp 10

3

KK

Kuro Kazuya

29 tháng 12 2016

Bài 1a)

Áp dụng bất đẳng thức Cô-si cho từng cặp ta có

\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)

\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)

\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)

\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )

Bài 1b)

Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)

\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )

Bài 1c) Ta có

\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)

\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)

\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)

\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)

Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)

\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )

KK

Kuro Kazuya

29 tháng 12 2016

Bài 2a)

Áp dụng bất đẳng thức Cô-si cho từng cặp ta có

\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)

\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)

\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )

Bài 2b)

Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)

Áp dụng BĐT Cô-si cho vế trái ta có

\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)

\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )

Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)

\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)

\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)

\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)

\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)

\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)

Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)

\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )

GT

™Gà●๖ۣۜNℊố●²ᵏ⁸ (ツтєαм♕¢âи♕6 ᴾᴿᴼシ)

18 tháng 2 2020 - olm

Tìm tập xác định các hàm số:

#Toán lớp 10

6

DD

๖ۣۜDương ๖ۣۜĐức๖ۣۜ Đạtღ ツ

18 tháng 2 2020

bài đâu bn ơi

G

ღŤ.Ť.Đღ

18 tháng 2 2020

Cko cái bài xem nào