Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)

1.
Không gian mẫu: \(8!\)
Xếp Quân Lâm cạnh nhau: \(2!\) cách
Coi cặp Quân-Lâm như 1 bạn, hoán vị với 6 bạn còn lại: \(7!\) cách
\(\Rightarrow2!.7!\) cách xếp thỏa mãn
Xác suất: \(P=\dfrac{2!.7!}{8!}=\dfrac{1}{4}\)
2.
Không gian mẫu: \(C_{12}^3\)
Lấy 3 bóng sao cho ko có bóng tốt nào (cả 3 đều là bóng ko tốt): \(C_4^3\) cách
\(\Rightarrow C_{12}^3-C_4^3\) cách lấy 3 bóng sao cho có ít nhất 1 bóng tốt
Xác suất: \(P=\dfrac{C_{12}^3-C_4^3}{C_{12}^3}=...\)
3.
Số tam giác bằng với số cách chọn 3 điểm từ 4 điểm nên có: \(C_4^3=...\) tam giác
4.
\(T_{\overrightarrow{v}}\left(E\right)=F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}x=-3+1=-2\\y=5-2=3\end{matrix}\right.\) \(\Rightarrow\left(-2;3\right)\)
5.
Có 2 cạnh chéo nhau với AB là SC, SD

Đáp án A
Phương pháp:
+) Biểu diễn không gian mẫu dưới dạng tập hợp
![]()
tìm Ω
+) Gọi A là biến cố: “Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”, biểu diễn A dưới dạng tập hợp và tìm số phần tử của A.
+) Tính xác suất của biến cố A: P(A) = A Ω
Cách giải:
Không gian mẫu
![]()
Có 9 cách chọn x, 9 cách chọn y, do đó Ω = 9.9 = 81
Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2 là hình tròn tâm O bán kính 2.
Gọi A là biến cố: “ Tập hợp các điểm mà khoảng cách đến gốc tọa độ nhỏ hơn hoặc bằng 2”
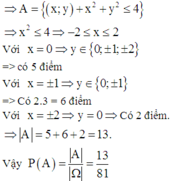

Chọn ngẫu nhiên 3 trong số 24 đỉnh của một đa giác đều 24 cạnh có \({C}_{24}^3 = 2024\)
\( \Rightarrow n\left( \Omega \right) = 2024\)
Gọi \(A\) là biến cố: “3 đỉnh được chọn là 3 đỉnh của một tam giác cân”, \(B\) là biến cố “3 đỉnh được chọn là 3 đỉnh của một tam giác vuông”.
Vậy \(AB\) là biến cố “3 đỉnh được chọn là 3 đỉnh của một tam giác vuông cân”, \(A \cup B\) là biến cố “3 đỉnh được chọn là 3 đỉnh của một tam giác cân hoặc một tam giác vuông”.
Gọi \(\left( O \right)\) là đường tròn ngoại tiếp đa giác đều.
Mỗi tam giác vuông có 3 đỉnh là 3 đỉnh của đa giác thì cạnh huyền của tam giác vuông phải là đường kính của \(\left( O \right)\), do đó ta có 12 cách chọn đường kính.
Với mỗi cách chọn đường kính, ta có 22 cách chọn đỉnh góc vuông (22 đỉnh còn lại của đa giác)
Vậy số tam giác vuông thỏa mãn điều kiện là: \(12.22 = 264\) (tam giác).
\( \Rightarrow n\left( A \right) = 264 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{264}}{{2024}} = \frac{3}{{23}}\)
Mỗi tam giác cân có 3 đỉnh là 3 đỉnh của đa giác thì đường cao của tam giác cân phải là đường kính của \(\left( O \right)\).
Với mỗi một đỉnh trên \(\left( O \right)\), ta có 10 cách tạo ra tam giác cân (không là tam giác đều).
Vậy số tam giác cân (không là tam giác đều) thỏa mãn điều kiện là: \(10.24 = 240\) (tam giác).
Số tam giác đều có 3 đỉnh nằm trên \(\left( O \right)\) là: \(24:3 = 8\) (tam giác).
\( \Rightarrow n\left( B \right) = 240 + 8 = 248 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{{248}}{{2024}} = \frac{{31}}{{253}}\)
Có 12 cách chọn đường kính.
Với mỗi cách chọn đường kính, ta có 2 cách chọn đỉnh góc vuông để tạo thành tam giác vuông cân.
Vậy số tam giác vuông cân thỏa mãn điều kiện là: \(12.2 = 24\) (tam giác).
\( \Rightarrow n\left( {AB} \right) = 24 \Rightarrow P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{{24}}{{2024}} = \frac{3}{{253}}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{3}{{23}} + \frac{{31}}{{253}} - \frac{3}{{253}} = \frac{{61}}{{253}}\)

Chọn B
Ta có ![]()
Do đó ![]()
Ta cũng có ![]() => n(A) = 8
=> n(A) = 8
Vậy xác suất của biến cố A là P(A) = 8 21

Gọi A là biến cố chọn được 3 quả cân có tổng trọng lượng không vượt quá 9 kg.
Suy ra A có các trường hợp sau:
A = { (1, 2, 3); (1, 2, 4); (1, 2, 5); (1, 2, 6); (1, 3, 4); (1, 3, 5); (2, 3, 4)}
⇒P=7C38=18⇒P=7C83=18
Vậy xác suất để trọng lượng 3 quả cân được chọn không quá 9 kg là: 18

Chọn B
Số phần tử không gian mẫu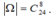
Gọi biến cố A = “Chọn 8 điểm sao cho không có 2 điểm nào có độ dài cung bằng 8 hoặc 3”.
Chia 24 điểm của đường tròn thành bảng sau:
1
9
17
4
12
20
7
15
23
10
18
2
13
21
5
16
24
8
19
3
11
22
6
14
Trong đó, mỗi cột là tập các số có cùng số dư khi chia 3, mỗi hàng là tập các số có cùng số dư khi chia 8. Nhận thấy, mỗi cột không được chọn quá 4 số vì chọn từ 5 số trở lên, sẽ xuất hiện 2 số kề nhau tạo cung có độ dài là 3.
TH1: Chọn 4 số của cột 1 không kề nhau: 2 cách là {1;7;13;19} hoặc {4;10;16;22}
1
9
17
4
12
20
7
15
23
10
18
2
13
21
5
16
24
8
19
3
11
22
6
14
Tiếp theo, chọn 4 số a,b,c,d còn lại không nằm cùng hàng với 4 số của cột 1 và 2 số bất kỳ trong 4 số a,b,c,d cũng không được cùng hàng với nhau, có 2 4 cách chọn.
Vậy có 2. 2 4 = 32cách.
TH2: Chọn 3 số của cột 1 sao cho không có 2 số nào kề nhau: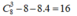
VD chọn{1;7;16} thì 5 số còn lai sẽ thuộc 3 nhóm màu trắng như hình vẽ. Khi đó mỗi nhóm màu trắng trong bảng chỉ có 2 cách chọn. Do đó TH2 có 16.2.2.2=128 cách.
TH3: Chọn 2 số không kề nhau của cột 1: C 8 2 - 8 = 20
Khi đó, 6 hàng ngang còn lai chia làm 2 nhóm màu trắng như hình vẽ. Mỗi nhóm có đúng 2 cách chọn nên có 20.2.2 = 80 cách.
TH4: Chọn 1 số của cột 1 có 8 cách
TH5: Chỉ chọn cột 2 với 3. Ta có 2 cách chọn là các dòng xanh hoặc trắng: 2 cách.