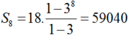Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

u 1 = 18 , u 2 = 54 ⇒ q = u 2 u 1 = 3.
Lại có u n = 39366 ⇔ u 1 . q n − 1 = 39366 ⇔ 18.3 n − 1 = 39366 ⇔ 3 n − 1 = 3 7 ⇔ n = 8
Vậy S 8 = 18. 1 − 3 8 1 − 3 = 59040
Chọn đáp án B.

Theo giả thiết ta có :
\(u_1+u_2=u_1+\frac{1}{4}\left(u_1\right)=24\)
\(\Rightarrow u_1+\frac{1}{4}u_1^2-24=0\)
\(\Leftrightarrow u_1=-12\) V \(u_1=8\)
Vậy có 2 cấp số nhân tương ứng là : 8,16,32,128 hoặc -12,36,-108,-972

a)
Gọi q là công bội của \(\left(u_n\right)\). Ta có:
\(\left\{{}\begin{matrix}u_1+u_1q^4=51\\u_1q+u_1q^5=102\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1+u_1q^4}{u_1q_1+u_1q^5}=\dfrac{51}{102}\)\(\Leftrightarrow\dfrac{1+q^4}{q+q^5}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1+q^4}{q\left(1+q^4\right)}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1}{q}=\dfrac{1}{2}\)\(\Leftrightarrow q=2\).
Suy ra: \(u_1+2^4u_1=51\)\(\Leftrightarrow17u_1=51\)\(\Leftrightarrow u_1=3\).
b) \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\)\(\dfrac{3\left(1-2^n\right)}{1-2}=3\left(2^n-1\right)=3069\)
\(\Leftrightarrow2^n-1=1023\)\(\Leftrightarrow2^n=1024=2^{10}\)\(\Leftrightarrow n=10\).
Vậy tổng của 10 số hạng đầu tiên bằng 10.
c)
Có \(u_1.q^{n-1}=3.2^{n-1}=12288\)\(\Leftrightarrow2^{n-1}=4096=2^{12}\)\(\Leftrightarrow n-1=12\)\(\Leftrightarrow n=13\).
Vậy số hạng thứ 13 bằng 12 288.

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Chọn B.
u1 = 18, u2 = 54 ⇒ q = 3
un = 39366 ⇔ u1.qn-1 = 39366 ⇔ 18.3n-1 = 39366 ⇔ 3n-1 = 37 ⇔ n = 8.
Vậy