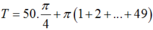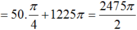Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\int\frac{1+sin2x+cos2x}{sinx+cosx}dx\)
\(=\int\frac{sin^2x+cos^2x+2sinxcosx+cos^2x-sin^2x}{sinx+cosx}dx\)
\(=\int\frac{\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(cosx+sinx\right)}{sinx+cosx}dx\)
\(=\int\left(sinx+cosx+cosx-sinx\right)dx=\int2cosxdx=2sinx\)
1.a/ \(\left\{{}\begin{matrix}3^{x+1}>0\\5^{x^2}>0\end{matrix}\right.\) \(\forall x\) \(\Rightarrow\) pt vô nghiệm
b/ Mình làm câu b, câu c bạn tự làm tương tự, 3 câu này cùng dạng
Lấy ln hai vế:
\(ln\left(3^{x^2-2}.4^{\dfrac{2x-3}{x}}\right)=ln18\Leftrightarrow ln3^{x^2-2}+ln4^{\dfrac{2x-3}{x}}-ln18=0\)
\(\Leftrightarrow\left(x^2-2\right)ln3+\dfrac{2x-3}{x}2ln2-ln\left(2.3^2\right)=0\)
\(\Leftrightarrow x^3ln3-2x.ln3+4x.ln2-6ln2-x.ln2-2x.ln3=0\)
\(\Leftrightarrow x^3ln3-4x.ln3+3x.ln2-6ln2=0\)
\(\Leftrightarrow x.ln3\left(x^2-4\right)+3ln2\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2ln3+2x.ln3+3ln2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\Rightarrow x=2\\x^2ln3+2x.ln3+3ln2=0\left(1\right)\end{matrix}\right.\)
Xét (1): \(\left(x^2+2x\right)ln3=-3ln2\Leftrightarrow x^2+2x=\dfrac{-3ln2}{ln3}=-3log_32\)
\(\Leftrightarrow\left(x+1\right)^2=1-3log_32=log_33-log_38=log_3\dfrac{3}{8}< 0\)
\(\Rightarrow\left(1\right)\) vô nghiệm
\(\Rightarrow\) pt có nghiệm duy nhất \(x=2\)
2/ Pt đã cho tương đương:
\(2017^{sin^2x}-2017^{cos^2x}=cos^2x-sin^2x\)
\(\Leftrightarrow2017^{sin^2x}+sin^2x=2017^{cos^2x}+cos^2x\)
Xét hàm \(f\left(t\right)=2017^t+t\) (\(0\le t\le1\))
\(\Rightarrow f'\left(t\right)=2017^t.ln2017+1>0\) \(\forall t\) \(\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow f\left(t_1\right)=f\left(t_2\right)\Leftrightarrow t_1=t_2\)
\(\Rightarrow sin^2x=cos^2x\Rightarrow cos^2x-sin^2x=0\Rightarrow cos2x=0\)
\(\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Thế k=0; k=1 ta được 2 nghiệm thuộc đoạn đã cho là \(x=\dfrac{\pi}{4};x=\dfrac{3\pi}{4}\)
\(\Rightarrow\) tổng nghiệm là \(T=\dfrac{\pi}{4}+\dfrac{3\pi}{4}=\pi\)
Câu 1: Là \(ln^2x+lnx\) hay \(lnx^2+lnx\) bạn, hai cái này khác nhau lắm, viết thế kia chẳng hiểu gì cả. Biểu thức logarit nếu viết mũ, thì hoặc là viết thế này \(ln^2x\) hoặc là \(\left(lnx\right)^2\), nếu viết \(ln\left(x\right)^2\) người ta sẽ mặc định hiểu là \(ln\left(x^2\right)\)
Chắc là cái đầu, vậy ta biến đổi được:
\(lnx\left(lnx+1\right)=lnx\left(lnx+lne\right)=lnx.ln\left(x.e\right)=ln\left(x.e\right)^{lnx}\)
Câu 2: đạo hàm 4 cái ra, dễ dàng nhận ra ở đáp án d, với \(x\ge0\Rightarrow f'\left(x\right)=3x^2+4x+\frac{1}{2\sqrt{x}}>0\) luôn đồng biến nên hàm không có cực trị
Câu 3:
Phương trình hoành độ giao điểm:
\(\frac{m-x}{x+1}=2x+m\Leftrightarrow m-x=2x^2+\left(m+2\right)x+m\)
\(\Leftrightarrow2x^2+\left(m+3\right)x=0\)
Phương trình luôn có nghiệm \(x=0\) hay ít nhất 1 trong 2 điểm A; B sẽ trùng gốc tọa độ tức \(OA=0\) hoặc \(OB=0\)
Do đó ko tồn tại m thỏa mãn
Câu 4:
\(\left\{{}\begin{matrix}lnx=X\\lny=Y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2X^2+3Y^2=5\\X+4Y=3\end{matrix}\right.\)
\(\Rightarrow2\left(3-4Y\right)^2+3Y^2=5\)
\(\Leftrightarrow35Y^2-48Y+13=0\Rightarrow\left[{}\begin{matrix}Y=1\Rightarrow X=-1\\Y=\frac{13}{35}\Rightarrow X=\frac{53}{35}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}lnx=-1\\lny=1\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(e^{-1};e\right)\) \(\Rightarrow\left\{{}\begin{matrix}c=-1\\d=1\end{matrix}\right.\)
Hoặc \(\left\{{}\begin{matrix}lnx=\frac{53}{35}\\lny=\frac{13}{35}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=e^{\frac{53}{35}}=e\sqrt[35]{e^{18}}\\y=e^{\frac{13}{35}}=\sqrt[35]{e^{13}}\end{matrix}\right.\) \(\Rightarrow a=b=35\)
Đáp án b sai
Chọn A.
Phương trình 
Xét hàm số f(t) = 2017t + t ; ta có f’(t) = 2017tln2017 + 1 > 0 mọi x
Suy ra hàm số đồng biến trên R.
Nhận thấy (*) có dạng f( sin2x) = f(cos2x) ; do đó: sin2x = cos2x
Vì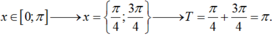 
Với điều kiện \(\left(m-2\cos x\right)\left(m-2\sin x\right)\ne0\) (*) phương trình đã cho tương đương với
\(\left(m\sin x-2\right)\left(m-2\sin x\right)=\left(m\cos x-2\right)=\left(m-2\cos x\right)\)
\(\Leftrightarrow m^2\sin x-2m-2m\sin^2x+4\sin x=m^2\cos x-2m-2m\cos^2x+4\cos x\)
\(\Leftrightarrow2m\left(\cos^2x-\sin^2x\right)-m^2\left(\cos x-\sin x\right)-4\left(\cos x-\sin x\right)=0\)
\(\Leftrightarrow\left(\cos x-\sin x\right)\left(2m\left(\cos x+\sin x\right)-m^2-4\right)=0\) (1)
a) Nếu \(m=0\) thì (1) \(\Leftrightarrow\cos x-\sin x=0\)\(\Leftrightarrow\tan x=1\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\). Nghiệm này sẽ không thỏa mãn điều kiện (*) khi và chỉ khi \(\left(m-2\cos\left(\dfrac{\pi}{4}+k\pi\right)\right)\left(m-2\sin\left(\dfrac{\pi}{4}+k\pi\right)\right)=0\)
\(\Leftrightarrow\left(0-\left(-1\right)^k\sqrt{2}\right)\left(0-\left(-1\right)^k\sqrt{2}=0\right)\)
\(\Leftrightarrow\left(-1\right)^k\sqrt{2}=0\) , vô lí.
Vậy khi \(m=0\), phương trình đã cho có nghiệm là \(x=\dfrac{\pi}{4}+k\pi\)
b) Nếu \(m\ne0\) thì (1) tương đương với tập hợp hai phương trình:
\(\tan x=1\) (2) và \(\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{m^2+4}{2m}\)\(\Leftrightarrow\cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{m^2+4}{2m\sqrt{2}}\) (3)
Trong đó phương trình (3) vô nghiệm vì \(\left|\dfrac{m^2+4}{2m\sqrt{2}}\right|=\dfrac{m^2+4}{2\sqrt{2}\left|m\right|}\ge\dfrac{2\sqrt{4m^2}}{2\sqrt{2}\left|m\right|}=\sqrt{2}>1\).
Phương trình (2) có nghiệm là \(x=\dfrac{\pi}{4}+k\pi\). Nghiệm này sẽ không thỏa mãn điều kiện (*) khi và chỉ khi
\(\left(m-2\cos\left(\dfrac{\pi}{4}+k\pi\right)\right)\left(m-2\sin\left(\dfrac{\pi}{4}+k\pi\right)\right)=0\)\(\Leftrightarrow\left(m-\left(-1\right)^k\sqrt{2}\right)\left(m-\left(-1\right)^k\sqrt{2}=0\right)\)
\(\Leftrightarrow m=\left(-1\right)^k\sqrt{2}\), trái giả thiết \(m\ne\pm\sqrt{2}\).
Tóm lại, trong mọi trường hợp phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+k\pi\) Điều kiện \(x\in[20\pi;30\pi]\) tương đương với \(20\pi\le\dfrac{\pi}{4}+k\pi\le30\pi\)\(\Leftrightarrow20-\dfrac{1}{4}\le k\le30-\dfrac{1}{4}\)\(\Leftrightarrow k=21;22;23;...;29\). Số nghiệm của phương trình trong đoạn đang xét là 9.
Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
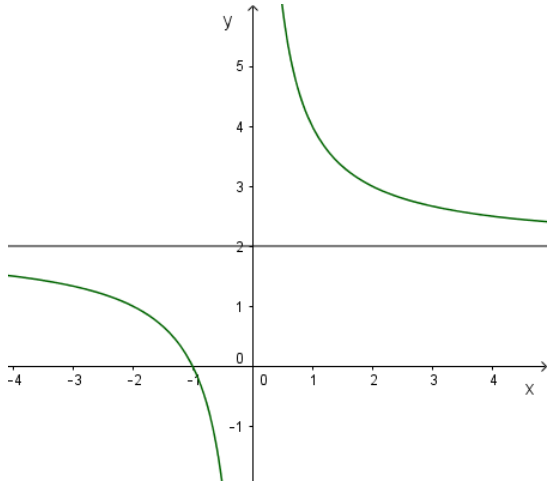
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
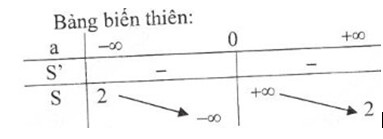
- Tập xác định : (-∞, 0)∪ (0, +∞)
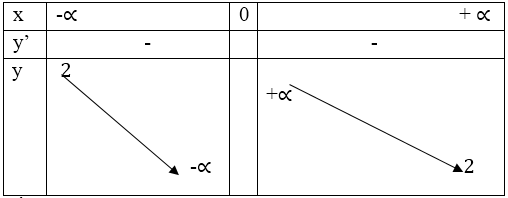
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
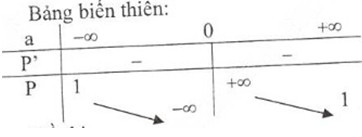
- Bảng biến thiên:
Đồ thị hàm số:
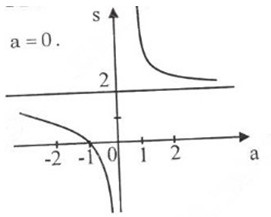
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
Đồ thị hàm số:
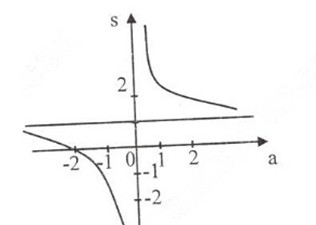
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.
Chọn B.
Điều kiện :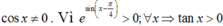
Ta có
Xét hàm số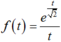
có 
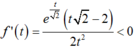với mọi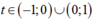 
Suy ra f(t) là hàm số nghịch biến trên khoảng (-1; 0) và (0; 1)
Mà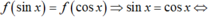
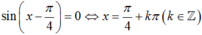
Lại có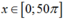
nên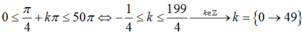 
Vậy tổng cần tính là
