Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

a ) \(\frac{7}{19}.\frac{8}{11}+\frac{3}{11}.\frac{7}{19}+\frac{-12}{19}\)
\(=\frac{7}{19}.\left(\frac{8}{11}+\frac{3}{11}\right)+\frac{-12}{19}\)
\(=\frac{7}{19}.\frac{11}{11}+\frac{-12}{19}\)
\(=\frac{7}{19}.1+\frac{-12}{19}\)
\(=\frac{7}{19}+\frac{-12}{19}\)
\(=\frac{7+\left(-12\right)}{19}\)
\(=-\frac{5}{19}\)
b ) \(\frac{-7}{25}.\frac{39}{-14}.\frac{50}{78}=\frac{-7.39.50}{25.-14.78}=\frac{-1.1.2}{1.-2.2}=\frac{-2}{-4}=\frac{1}{2}\)
c ) \(\left(\frac{3}{8}+\frac{-3}{4}+\frac{7}{12}\right):\frac{5}{6}+\frac{1}{2}\)
\(=\frac{5}{24}:\frac{5}{6}+\frac{1}{2}\)
\(=\frac{5}{24}.\frac{6}{5}+\frac{1}{2}\)
\(=\frac{1}{4}+\frac{1}{2}\)
\(=\frac{3}{4}\)
a)\(\frac{7}{19}.\frac{8}{11}+\frac{3}{11}.\frac{7}{19}+\frac{-12}{19}=\frac{7}{19}.\frac{8}{11}+\frac{3}{11}.\frac{7}{19}+\frac{7}{19}.\frac{-12}{7}=\frac{7}{19}.\left(\frac{8}{11}+\frac{3}{11}+-\frac{12}{7}\right)=\frac{7}{19}.\left(\frac{-5}{7}\right)=-\frac{5}{19}\)
b)\(\frac{-7}{25}.\frac{39}{-14}.\frac{50}{78}=\frac{\left(-7\right).39.50}{25.\left(-14\right).78}=\frac{\left(-7\right).3.13.2.5.5}{5.5.\left(-7\right).2.2.13.3}=\frac{1}{2}\)
c)\(\left(\frac{3}{8}+\frac{-3}{4}+\frac{7}{12}\right):\frac{5}{6}+\frac{1}{2}=\frac{5}{24}:\frac{5}{6}+\frac{1}{2}=\frac{2}{7}+\frac{1}{2}=\frac{11}{14}\)

\(\frac{5}{6}.\frac{4}{19}+\frac{-7}{12}.\frac{4}{19}-\frac{40}{57}\)
\(=\frac{4}{19}.\left(\frac{5}{6}+\frac{-7}{12}\right)-\frac{40}{57}\)
\(=\frac{4}{19}.\frac{1}{4}-\frac{40}{57}\)
\(=\frac{1}{19}-\frac{40}{57}\)
\(=\frac{43}{57}\)

Đặt mỗi số số hạng của M là A;B
Ta quy đồng tử và mẫu của A bằng cách nhân cả tử và mẫu với 3.7.13;rồi dùng tính chất phân phối bỏ ngoặc ra.Tính toán bình thường.Khi đó A=1/7
Tương tự với B ta quy đồng lên với 11.17.19;bỏ ngoặc đi và tính bình thường ;B=2/7
=>M=1/7+2/7-136/7=3/7-136/7=-19

Cách 1 : A=100+98+96+...+2-97-95-...-1
A= 100 + (98-97) + (96-95) + ... +(2-1)
Từ 1 đến 98 có 98 số => có 98 : 2 cặp mà hiệu = 1
A = 100 + 49 x 1 = 149
B = 1+2-3-4+5+6-7-8+9+10-11-12+...-299-300+301+302
B = 1 + 2 + (302 - 300) + (301 - 299) + ... + (10 - 8) + (9-7) + (6-4) + (5-3)
Từ 3 đến 302 có 300 số => có 300 : 2 cặp hiệu = 2
B = 1 + 2 + 150 x 2 = 303
Cách 2 :
A = 100 + (98-97) + (96-95) + ……. + (2-1)
Ta thấy: 97; 95; ….; 1 có (97 – 1) : 2 + 1 = 49 (số hạng)
A = 100 + (1+1+1+….+1) (có 49 số 1).
A = 100 + 49 = 149
a, A = 100+(98-97)+(86-95)+....+(2-1) = 100+1+1+...+1 (49 số 1) = 149
b, B = 1+(2-3-4+5)+(6-7-8+9)+....(297-298-299+330)+331-332
= 1+0+0+....+0+331-332 = 0
Nếu đúng thì k mk nha

A =\(\frac{7}{19}.\frac{8}{11}+\frac{7}{19}.\frac{3}{11}+\frac{12}{19}\)
A = \(\frac{7}{19}.\left(\frac{8}{11}+\frac{3}{11}\right)\)+ \(\frac{12}{19}\)
A = \(\frac{7}{19}.1+\frac{12}{19}\)
A = \(\frac{7}{19}+\frac{12}{19}\)
A = 1
--------
B = \(\frac{5}{9}.\frac{7}{13}+\frac{5}{9}.\frac{9}{13}-\frac{5}{9}.\frac{3}{13}\)
B = \(\frac{5}{9}.\left(\frac{7}{13}+\frac{9}{13}-\frac{3}{13}\right)\)
B = \(\frac{5}{9}.1\)
B = \(\frac{5}{9}\)
-------
C = \(\left(\frac{67}{111}+\frac{2}{33}-\frac{15}{117}\right).\left(\frac{1}{3}-\frac{1}{4}-\frac{1}{12}\right)\)
C = \(\left(\frac{67}{111}+\frac{2}{33}-\frac{15}{117}\right).\left(\frac{4}{12}-\frac{3}{12}-\frac{1}{12}\right)\)
C = \(\left(\frac{67}{111}+\frac{2}{33}-\frac{15}{117}\right).0\)
C = 0
Chúc bạn học tốt

\(A=\dfrac{7}{19}\cdot\dfrac{8}{11}+\dfrac{7}{11}\cdot\dfrac{3}{11}\\ =\dfrac{7\cdot8}{19\cdot11}+\dfrac{7}{11}\cdot\dfrac{3}{11}\\ =\dfrac{8}{19}\cdot\dfrac{7}{11}+\dfrac{7}{11}\cdot\dfrac{3}{11}\\ =\dfrac{7}{11}\cdot\left(\dfrac{8}{19}+\dfrac{3}{11}\right)\\ =\dfrac{7}{11}\cdot\dfrac{145}{209}\\ =\dfrac{1015}{2299}\)

\(=\frac{7}{19}.\left(\frac{8}{11}+\frac{3}{11}\right)+\frac{12}{19}\)
\(=\frac{7}{19}.1+\frac{12}{19}\)
\(=1\)
\(\frac{7}{19}\).\(\frac{8}{11}\)+\(\frac{7}{19}\).\(\frac{3}{11}\)+\(\frac{12}{19}\)
=\(\frac{7}{19}\).1+\(\frac{12}{19}\)
=1
hok tốt
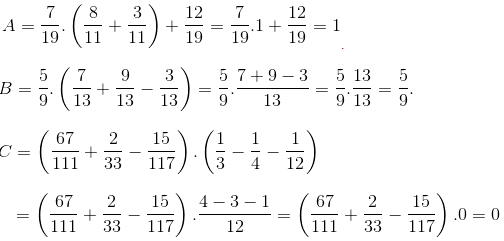
Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.