Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1a/ \(\left(15-x\right)+\left(x-12\right)=7-\left(-5+x\right)\)
=> \(\left(15-x\right)+\left(x-12\right)+\left(-5+x\right)=7\)
=> \(15-x+x-12-5+x=7\)
=> \(\left(15-12-5\right)-\left(x+x+x\right)=7\)
=> \(\left(15-12-5\right)-7=3x\)
=> \(3x=-2-7\)
=> \(3x=-9\)
=> \(x=\frac{-9}{3}=-3\)
b/ \(x-\left\{57-\left[42+\left(-23-x\right)\right]\right\}=13-\left\{47+\left[25-\left(32-x\right)\right]\right\}\)
=> \(x-57-42-23-x=13-47+25-32+x\)
=> \(x-x+x=13-47+25-32+57+42+23\)
=> \(x=\left(13+23\right)-\left(47+57\right)+\left(25+57\right)-\left(32+42\right)\)
=> \(x=36-104+82-74\)
=> \(x=-60\)
d/ \(\left(x-3\right)\left(2y+1\right)=7\)
Vì 7 là số nguyên tố nên ta có 2 trường hợp:
TH1: \(\hept{\begin{cases}x-3=1\\2y+1=7\end{cases}}\)=> \(\hept{\begin{cases}x=4\\y=3\end{cases}}\).
TH2: \(\hept{\begin{cases}x-3=7\\2y+1=1\end{cases}}\)=> \(\hept{\begin{cases}x=10\\y=0\end{cases}}\).
Các cặp (x, y) thoả mãn điều kiện: \(\left(4;3\right),\left(10;0\right)\).

a) \(2^x+5=21\)
\(\Rightarrow2^x=21-5=16\Rightarrow2^x=2^4\)
Vậy x = 4
b) \(2^x-1+3^2=5^2+2.5\)
\(\Rightarrow2^x-1+9=35\)
\(\Rightarrow2^x=35-9+1=27\)
Vậy x không có giá trị
c;d;e;f làm tương tự

B=\(6\frac{4}{9}-4\frac{4}{9}+3\frac{7}{11}\)
B=\(2+3\frac{7}{11}\)
B=\(5\frac{7}{11}\)
B = \(5\frac{7}{11}=\frac{62}{11}\)
C = 1
D = \(\frac{5}{2}=2\frac{1}{2}\)

a) \(\frac{2}{5}x-x=\frac{\left(-2018\right)^0}{5^2}\\ x\left(\frac{2}{5}-1\right)=\frac{1}{25}\\ x\left(\frac{2}{5}-\frac{5}{5}\right)=\frac{1}{25}\\ x\cdot\frac{-3}{5}=\frac{1}{25}\\ x=\frac{1}{25}:\frac{-3}{5}\\ x=\frac{1}{25}\cdot\frac{-5}{3}\\ x=\frac{-1}{15}\)Vậy \(x=\frac{-1}{15}\)
b) \(\left|-1\frac{1}{2}x+2x\right|-\frac{7}{4}=0,5\\ \left|x\left(-1\frac{1}{2}+2\right)\right|-\frac{7}{4}=\frac{1}{2}\\ \left|x\cdot\frac{1}{2}\right|=\frac{1}{2}+\frac{7}{4}\\ \left|x\cdot\frac{1}{2}\right|=\frac{2}{4}+\frac{7}{4}\\ \left|x\cdot\frac{1}{2}\right|=\frac{9}{4}\\ \Rightarrow\left[{}\begin{matrix}x\cdot\frac{1}{2}=\frac{9}{4}\\x\cdot\frac{1}{2}=\frac{-9}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{9}{4}:\frac{1}{2}\\x=\frac{-9}{4}:\frac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{9}{4}\cdot2\\x=\frac{-9}{4}\cdot2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{9}{2}\\x=\frac{-9}{2}\end{matrix}\right.\)Vậy \(x\in\left\{\frac{9}{2};\frac{-9}{2}\right\}\)
c) \(x+\left(x+\frac{2}{7}\right)+\frac{-5}{11}=\frac{4}{11}\\ x+x+\frac{2}{7}=\frac{4}{11}-\frac{-5}{11}\\ 2x+\frac{2}{7}=\frac{4}{11}+\frac{5}{11}\\ 2x+\frac{2}{7}=\frac{9}{11}\\ 2x=\frac{9}{11}-\frac{2}{7}\\ 2x=\frac{63}{77}-\frac{22}{77}\\ 2x=\frac{41}{77}\\ x=\frac{41}{77}:2\\ x=\frac{41}{77\cdot2}\\ x=\frac{41}{154}\)Vậy \(x=\frac{41}{154}\)
d) \(\left|0,25x-20\%\right|+\frac{3}{8}=1\frac{3}{8}\\ \left|\frac{1}{4}x-\frac{1}{5}\right|=1\frac{3}{8}-\frac{3}{8}\\ \left|\frac{1}{4}x-\frac{1}{5}\right|=1\\ \Rightarrow\left[{}\begin{matrix}\frac{1}{4}x-\frac{1}{5}=1\\\frac{1}{4}x-\frac{1}{5}=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\frac{1}{4}x=1+\frac{1}{5}\\\frac{1}{4}x=\left(-1\right)+\frac{1}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\frac{1}{4}x=\frac{5}{5}+\frac{1}{5}\\\frac{1}{4}x=\frac{-5}{5}+\frac{1}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\frac{1}{4}x=\frac{6}{5}\\\frac{1}{4}x=\frac{-4}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{6}{5}:\frac{1}{4}\\x=\frac{-4}{5}:\frac{1}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{6}{5}\cdot4\\x=\frac{-4}{5}\cdot4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\frac{24}{5}\\x=\frac{-16}{5}\end{matrix}\right.\)Vậy \(x\in\left\{\frac{24}{5};\frac{-16}{5}\right\}\)

a) \(|x+1|=3\)
\(\Rightarrow x+1=\pm3\)
+) \(x+1=3\) +) \(x+1=-3\)
\(\Rightarrow x=2\) \(\Rightarrow x=-4\)
Vậy \(x\in\left\{2;-4\right\}\)
b) \(3^2x+2^4=5^2\)
\(9x+16=25\)
\(9x=25-16\)
\(9x=9\)
\(x=1\)
c) \(\frac{4+x}{7+y}=\frac{4}{7}\)
\(\Rightarrow\left(4+x\right).7=\left(7+y\right).4\)
\(\Rightarrow28+7x=28+4y\)
\(\Rightarrow7x=4y\)
Mà \(\left(7,4\right)=1\) và \(x+y=11\)
Vậy \(x=4;y=7\)
a) Ta có: \(\left|x+1\right|=3\)
\(\Rightarrow x+1=\pm3\)
Nếu x + 1 = 3 => x = 2
Nếu x + 1 = -3 => x = -4
Vậy x = {2;-4}
b) \(3^2x+2^4=5^2\)
\(\Rightarrow9x+16=25\)
\(\Rightarrow9x=9\)
\(\Rightarrow x=1\)
Vậy x = 1
c) \(\frac{4+x}{7+x}=\frac{4}{7}\)
\(\Rightarrow7\left(4+x\right)=4\left(7+x\right)\)
\(\Rightarrow28+7x=28+4x\)
\(\Rightarrow7x-4x=0\)
\(\Rightarrow x=0\)
Vậy x = 0

a, Ta có : \(7^6+7^5-7^4\)
\(=7^4.7^2+7^4.7+7^4.1=7^4.49+7^4.7+7^4.1\)
\(=7^4.\left(49+7-1\right)\)
\(=7^4.55\) \(⋮\) \(55\) (vì \(55⋮55\))
Vậy \(7^6+7^5-7^4⋮55\)
b, Ta có : \(3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n.3^2-2^n.2^2+3^n-2^n\)
\(=\left(3^n.3^2+3^n\right)-\left(2^n.2^2+2^n\right)\)
\(=3^n.\left(3^2+1\right)-2^n.\left(2^2+1\right)\)
\(=3^n.\left(9+1\right)-2^n.\left(4+1\right)\)
\(=3^n.10-2^n.5\)
\(=3^n.2.5-2^{n-1}.2.5\)
\(=2.5.\left(3^n-2^{n-1}\right)\) chia hết cho 2 và 5( vì \(2⋮2\) ; \(5⋮5\) )
Vậy \(3^{n+2}-2^{n+2}+3^n-2^n\) chia hết cho 2 và 5
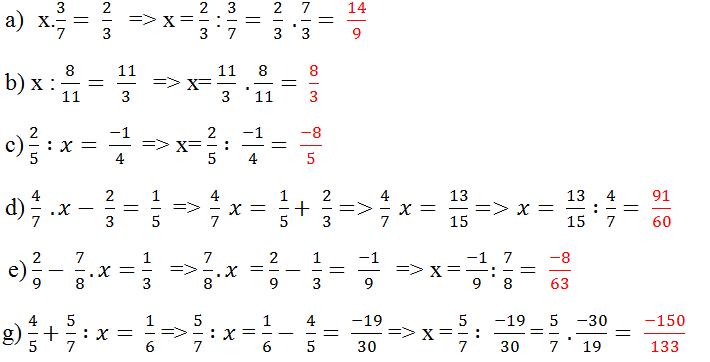
a, x - 1 2 = 36
ó x - 1 2 = 6 2
ó x – 1 = 6
ó x = 7
Vậy x = 7
b, 7 x - 11 3 = 2 5 . 5 2 + 200
=> 7 x - 11 3 = 800 + 200
=> 7 x - 11 3 = 1000
=> 7 x - 11 3 = 10 3
=> 7x – 11 = 10
=> 7x = 21
=> x = 3
Vậy x = 3
c, x 11 = x
=> x 11 - x = 0
=> x ( x 10 - 1 ) = 0
=>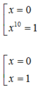
d, x 2 = 2 3 + 3 2 + 4 3
=> x 2 = 81
=> x = 9
e, 2 x 3 3 2 = 48
=> 2 x 3 9 = 48
=> 2 x 3 = 48 . 9
=> x 3 = 216
=> x 3 = 6 3
=> x = 6
f, 2 x + 1 3 = 125
=> 2 x + 1 3 = 5 3
=> 2x + 1 = 5
=> 2x = 4
=> x = 2