Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.
Ta có AD vuông góc với D1D vì A1D1DA là hình chữ nhật
Tương tự => DC cũng vuông góc với D1D
Mà AD chỉ vuông góc với DC vì ABCD là hình chữ nhật mà thôi chứ không song song
=> Mệnh đề trên là sai
(>Tích đúng cho mình nha<) 
Ta có: mp(ABCD) // mp(A1B1C1D1)
AB thuộc mp(ABCD)
A1D1 thuộc mp(A1B1C1D1)
AB không song song với A1D1
Vậy mệnh đề đã cho sai.
Ta có:AB ⊥ BC
C C 1 ⊥ BC
Nhưng AB và C C 1 không song song với nhau
Vậy mệnh đề đã cho là sai
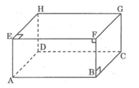Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song.
Vậy mệnh để b) sai.
Gt và câu c viết nhầm phải không bạn? Trung tuyến BD,CE,AM chứ. Còn câu b phải qua B kẻ đường thẳng // FD nhỉ? Nếu thế thì lời giải thế này
(lời giải hơi dài tí)
*Xét tứ giác DEMC:
\(ED=\frac{1}{2}BC\)(cma)
\(CM=\frac{1}{2}BC\)(gt)
\(\Rightarrow ED=CM\)
Mà ED//BC (Cma); \(M\in BC\left(gt\right)\)=> ED//CM
Từ 2 chứng minh trên => DEMC là hbh
=>CD//EM(1)
*Mặt khác, ta có: DF//CE(cmb); DF=CE(cmb)
DF//BP(cmc); DF=BP(cmc)
=> CE//BP(cùng //DF); CE=BP(cùng = DF)
Từ chứng minh trên => CEBP là hbh
Nên 2 đường chéo PE và CB cắt nhau tại trung điểm mỗi đường
Mà M là trung điểm CB (gt) => M cũng là trung điểm PE
hay P,M,E thẳng hàng(2)
Từ (1),(2) CD//EP
=> CDEP là hình thang
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
A B C D O K a)Xét tứ giác OBKC, ta có:
OC//BK(BK//AC)
BO//KC(KC//BD)
=>tứ giác OBKC là hình bình hành
lại có:
AC \(\perp\) BD ( hai đường chéo)
BD//KC
=> \(\)góc OCK =90o
=> hình bình hành OBKC là hình chữ nhật
b)Ta có:
BC = OK ( do OCKD là hình chữ nhật)
AB=BC( cách cạnh hình thoi bằng nhau)
=> AB = OK
c)
* nếu tứ giác ABCD là hình vuông:
=>BD=AC
mà: BO=1/2BD
OC=1/2AC
=> BO = OC
=> hình chữ nhật OBKC là hình vuông.
Vậy HCN OBKC là hình vuông khi hình thoi ABCD là hình vuông
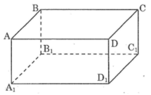
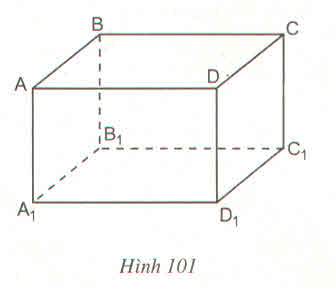
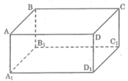
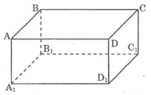
Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a) sai.