
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

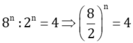
![]()

Với \(x=0\Rightarrow n^5+n^4+1=1\left(loai\right)\)
Với \(x=1\Rightarrow n^5+n^4+1=3\left(TM\right)\)
Với \(x\ge2\) ta có:
\(n^5+n^4+1\)
\(=n^5-n^2+n^4-n+n^2+n+1\)
\(=n^2\left(n^3-1\right)+n\left(n^3-1\right)+\left(n^2+n+1\right)\)
\(=n^2\left(n-1\right)\left(n^2+n+1\right)+n\left(n-1\right)\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=A\cdot\left(n^2+n+1\right)+B\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=\left(n^2+n+1\right)\left(A+B+1\right)\) là hợp số với mọi \(n\ge2\)
Vậy \(n=1\)
Với \(n=0\Rightarrow A=n^8+n+1=1\left(KTM\right)\) vì 1 không là SNT
Với \(n=1\Rightarrow A=n^8+n+1=3\left(TM\right)\) vì 3 là SNT
Với \(n\ge2\) ta có:
\(A=n^8+n+1\)
\(=\left(n^8-n^2\right)+n^2+n+1\)
\(=n^2\left(n^6-1\right)+\left(n^2+n+1\right)\)
\(=n^2\left[\left(n^3\right)^2-1^2\right]+\left(n^2+n+1\right)\)
\(=n^2\left(n^3-1\right)\left(n^3+1\right)+\left(n^2+n+1\right)\)
\(=X\cdot\left(n^3-1\right)+\left(n^2+n+1\right)\)
\(=X\left(n-1\right)\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=X'\left(x^2+n+1\right)+\left(n^2+n+1\right)\)
\(=\left(n^2+n+1\right)\left(X'+1\right)\) là hợp số với \(n\ge2\)
Vậy \(n=1\)

\(a,\frac{16}{2^n}=2\Rightarrow2^n=16:2\Rightarrow2^n=8\Rightarrow2^n=2^3\Rightarrow n=3\)
\(b,\frac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=81.\left(-27\right)\Rightarrow\left(-3\right)^n=-2187\Rightarrow3^n=3^7\Rightarrow n=7\)
\(c,8^n:2^n=4\Rightarrow4^n=4\Rightarrow n=1\)
\(a,\frac{16}{2^n}=2\) \(b,\frac{\left(-3\right)^n}{81}=-27\) \(c,8^n:2^n=4\)
\(\Rightarrow2^4=2^n.2\) \(\Rightarrow\left(-3\right)^n=\left(-27\right).81\) \(\Rightarrow\left(8:2\right)^n=4\)
\(\Rightarrow4=n+1\) \(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\) \(\Rightarrow4^n=4\)
\(\Rightarrow n=4-1=3\) \(\Rightarrow n=7\) \(\Rightarrow n=1\)

a) 162n=2 => \(\dfrac{2^4}{2^n}=2\Rightarrow2^{4-n}=2\Rightarrow4-n=1\Rightarrow n=3\)
b,
\(\dfrac{\left(-3\right)^n}{81}=-27\Rightarrow\dfrac{\left(-3\right)^n}{\left(-3\right)^4}=-27\Rightarrow\left(-3\right)^{n-4}=\left(-3\right)^3\Rightarrow n-4=3\Rightarrow n=7\)
c,\(8^n:2^n=4\Rightarrow4^n=4\Rightarrow n=1\)
 => (-3)n-4 = (-3)3
=> (-3)n-4 = (-3)3
=> n - 4 = 3 => n = 7
c) 8n : 2n = 4
4n = 4.

a)
\(\frac{16}{2^x}=2\)
\(\Rightarrow2^{x+1}=16\)
\(\Rightarrow2^{x+1}=2^4\)
\(\Rightarrow x+1=4\)
\(\Rightarrow x=3\)
b)
\(\frac{\left(-3\right)^x}{81}=-27\)
\(\Rightarrow\left(-3\right)^x=-\left(3^3.3^4\right)\)
\(\Rightarrow-3^x=-3^7\)
=> x=7
c)
\(8^n:2^n=4\)
\(\Rightarrow2^{3n}:2^n=4\)
\(\Rightarrow2^{3n-n}=4\)
\(\Rightarrow2^{2n}=2^2\)
=>2n=2
=>n=1
a)\(\frac{16}{2^n}=2\)
=>16:2n=2
=>2n=16:2
=>2n=8
b)ko nhớ cách làm
c)8n:2n=4
=>(23)n:2n=22
=>23n:2n=22
=>23n-n=22
=>22n=22
=>2n=2
=>n=1
dc rùi chứ


Đặt S = 2.22 + 3.23 + 4.24 + ... + (n - 1).2n - 1 + n.2n
<=> S = 2S - S = (2.23 + 3.24 + 4.25 + .... + (n - 1).2n + n. 2n + 1) - (2.22 + 3.23 + 4.24 + ... + (n - 1).2n - 1 + n.2n)
S = (2.23 - 3.23) + (3.24 - 4.24) + (4.25 - 5.25) + .... + [(n - 1).2n - n.2n] + n.2n + 1 - 2.22
= -(23 + 24 + 25 + ... + 2n) + n.2n + 1 - 8
Đặt A = 23 + 24 + 25 + ... + 2n
<=> 2A - A = (24 + 25 + 26 + ... + 2n + 1) - (23 + 24 + 25 + ... + 2n)
<=> A = 2n + 1 - 23
Khi đó S = - 2n - 1 + 23 + n.2n - 1 - 8
= 2n - 1.(n - 1) = 2n + 34
=> n - 1 = 2n + 34 : 2n - 1
=> n - 1 = 2n + 34 - n + 1
=> n - 1 = 235
=> n = 235 + 1
Tìm số tự nhiên n, biết:
a) \(\frac{16}{2^n}=2\)
b) \(\frac{\left(-3\right)^n}{81}=-27\)
c) \(8^n:2^2\)

a) \(\frac{16}{2^n}=2\)
=> 16 = 2 . 2n
=> 16 = 2n+1
=> 24 = 2n+1
=> n + 1 = 4
=> n = 4 - 1
=> n = 3
Vậy n = 3
b) \(\frac{\left(-3\right)^n}{81}=-27\)
=> (-3)n = -27 . 81
=> (-3)n = (-3)3 . (-3)4
=> (-3)n = (-3)7
=> n = 7
Vậy n = 7
c) 8n : 22 = bao nhiêu vậy ban?
Chuk bn hk tốt!![]()
a)\(\frac{16}{2^n}=2\)
\(\Rightarrow16:2=2^n\)
2n=8=23
Vậy n=3
b)\(\frac{\left(-3\right)^n}{81}=-27\)
\(\Rightarrow\)(-3)n=-27.81
(-3)n=-2187=(-3)7
Vậy n=7
c)Mk ko hiểu bn ghi gì

Giải thích các bước giải:
a. Vì DM⊥AB⇒ˆDMA=90oDM⊥AB⇒DMA^=90o,
DN⊥AC⇒ˆDNA=90oDN⊥AC⇒DNA^=90o,
ΔABC⊥A⇒ˆA=90oΔABC⊥A⇒A^=90o
⇒◊AMDN⇒◊AMDN là hình chữ nhật.
Áp dụng định lý Pitago vào ΔAMD⊥M,AM=3cm,AD=5cmΔAMD⊥M,AM=3cm,AD=5cm có:
MD=√AD2−AM2=4cmMD=AD2−AM2=4cm
⇒SAMDN=AM.DM=12cm2⇒SAMDN=AM.DM=12cm2
b. Gọi AD∩MN=E⇒EAD∩MN=E⇒E là trung điểm AD, MN
Mà AH⊥BCAH⊥BC
ΔAHD⊥H,EΔAHD⊥H,E là trung điểm cạnh huyền ADAD
⇒EH=EA=ED=EM=EN⇒EH=EA=ED=EM=EN
⇒ΔMHN⇒ΔMHN vuông tại HH
⇒ˆMHN=90o⇒MHN^=90o
c. Gọi G,IG,I là trung điểm AB,ACAB,AC suy ra GIGI là đường trung bình của ΔABCΔABC
⇒GI//BC⇒GI//BC
⇒GE,EI⇒GE,EI là đường trung bình ΔABD,ΔADC⇒GE//BD,EI//DCΔABD,ΔADC⇒GE//BD,EI//DC hay GE,EI//BCGE,EI//BC
⇒E∈GI⇒E∈GI
⇒⇒ Trung điểm EE của MNMN di chuyển trên đường trung bình ΔABCΔABC.

\(\frac{16}{2^n}=1;2^n=8;n=3\)
\(\frac{\left(-3\right)^n}{81}=-27;\left(-3\right)^n=\left(-3\right)^7;n=7\)
\(8^n:2^n=4;\left(8:2\right)^n=4;4^n=4=4^1;n=1\)