PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
CM
19 tháng 4 2019
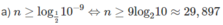
Vì n là số tự nhiên bé nhất nên n = 30.
b) n = 4
c) n = 16
d) n = 15
TN
0
20 tháng 10 2019
a
=>(n+2)=5 :.n+2
=>5:. n+2
=>n+2 E (1,5)
th1
N+2=1
th2 tựlamf
AM
6 tháng 9 2020
Câu 2. Đặt A=x2+y2+1
Nhập \(2^A=\left(A-2x+1\right)4^x\) vào máy tính Casio. Cho x=0.01, tìm A
Máy sẽ giải ra, A=1.02=1+2x
\(\Leftrightarrow x^2+y^2+1=1+2x\)
\(\Leftrightarrow x^2+y^2-2x=1\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=1\) (C)
Có (C) là đường tròn tâm (1,0) bán kính R=1
Lại có: P=\(\frac{8x+4}{2x-y+1}\)
\(\Leftrightarrow x\left(2P-8\right)-yP+P-4=0\) (Q)
Có (Q) là phương trình đường thẳng.
Để x,y có nghiệm thì đường thẳng và đường tròn giao nhau nghĩa là d(I,(Q))\(\le R\)
\(\Leftrightarrow\frac{\left|x\left(2P-8\right)-yP+P-4\right|}{\sqrt{\left(2P-8\right)^2+P^2}}\le1\)
\(\Leftrightarrow\frac{\left|2P-8+P-4\right|}{\sqrt{\left(2P-8\right)^2+1}}\le1\)
\(\Leftrightarrow\left(3P-12\right)^2\le5P^2-32P+64\)
\(\Leftrightarrow4P^2-40P+80\le0\)
\(\Leftrightarrow5-\sqrt{5}\le P\le5+\sqrt{5}\)
Vậy GTNN của P gần số 3 nhất. Chọn C
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2020
1/ \(f'\left(x\right)=\frac{3\sqrt{x^2+1}-\frac{x\left(3x+1\right)}{\sqrt{x^2+1}}}{x^2+1}=\frac{3\left(x^2+1\right)-3x^2-x}{\left(x^2+1\right)\sqrt{x^2+1}}=\frac{3-x}{\left(x^2+1\right)\sqrt{x^2+1}}\)
Hàm số đồng biến trên \(\left(-\infty;3\right)\) nghịch biến trên \(\left(3;+\infty\right)\)
\(\Rightarrow f\left(x\right)\) đạt GTLN tại \(x=3\)
\(f\left(x\right)_{max}=f\left(3\right)=\frac{10}{\sqrt{10}}=\sqrt{10}\)
2/ \(y'=\frac{\sqrt{x^2+2}-\frac{\left(x-1\right)x}{\sqrt{x^2+2}}}{x^2+2}=\frac{x^2+2-x^2+x}{\left(x^2+2\right)\sqrt{x^2+2}}=\frac{x+2}{\left(x^2+2\right)\sqrt{x^2+2}}\)
\(f'\left(x\right)=0\Rightarrow x=-2\in\left[-3;0\right]\)
\(y\left(-3\right)=-\frac{4\sqrt{11}}{11}\) ; \(y\left(-2\right)=-\frac{\sqrt{6}}{2}\) ; \(y\left(0\right)=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}M=-\frac{\sqrt{2}}{2}\\N=-\frac{\sqrt{6}}{2}\end{matrix}\right.\) \(\Rightarrow MN=\frac{\sqrt{12}}{4}=\frac{\sqrt{3}}{2}\)
Tất cả các đáp án đều sai
3/ \(\left\{{}\begin{matrix}\left|x-3\right|\ge0\\\sqrt{x+1}>0\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\ge0\) \(\forall x\Rightarrow N=0\) khi \(x=3\)
- Với \(0\le x< 3\Rightarrow f\left(x\right)=\left(3-x\right)\sqrt{x+1}\)
\(\Rightarrow f'\left(x\right)=-\sqrt{x+1}+\frac{\left(3-x\right)}{2\sqrt{x+1}}=\frac{-2\left(x+1\right)+3-x}{2\sqrt{x+1}}=\frac{-3x+1}{2\sqrt{x+1}}\)
\(f'\left(x\right)=0\Rightarrow x=\frac{1}{3}\)
- Với \(3< x\le4\Rightarrow f\left(x\right)=\left(x-3\right)\sqrt{x+1}\)
\(\Rightarrow f'\left(x\right)=\sqrt{x+1}+\frac{x-3}{2\sqrt{x+1}}=\frac{2\left(x+1\right)+x-3}{2\sqrt{x+1}}=\frac{3x-1}{2\sqrt{x+1}}>0\) \(\forall x>3\)
Ta có: \(f\left(0\right)=3\) ; \(f\left(\frac{1}{3}\right)=\frac{16\sqrt{3}}{9}\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow M=\frac{16\sqrt{3}}{9}\Rightarrow M+2N=\frac{16\sqrt{3}}{9}\)
TT
3 tháng 4 2020
Câu 2 hình như câu B mà người ta nói đạt GTLN . GTNN tại M , N nên là 0 x -2 =0
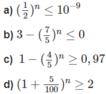
n ≥ log 1 2 10 - 9 ⇔ n ≥ 9 log 2 10 ≈ 29 , 897
Vì n là số tự nhiên bé nhất nên n = 30.