Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Điều kiện xác định: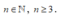 
.
Ta có: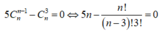 
.
.
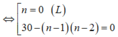Khi đó nhị thức Niu-tơn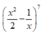 
có số hạng tổng quát:
.
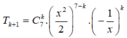
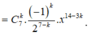Số hạng chứa x 5 có giá trị k thỏa mãn: 14 - 3k = 5 => k = 3.
Vậy hệ số của số hạng chứa
x
5
là: 
.
\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)
Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn
Vậy trong khai triển trên ko có số hạng chứa \(x^8\)
b/ \(\left(1-x^2+x^4\right)^{16}\)
\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)
\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)
Hệ số của số hạng chứa \(x^{16}\):
\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)
c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)
Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)
SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)
Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)
\(\sum_{k=1}^nC^k_{2n+1}=2^{20}-1\)
\(\frac{\sum_{k=1}^n\left(2C^k_{2n+1}\right)+1+1}{2}=2^{20}\)
\(C^0_{2n+1}+\sum_{k=1}^n\left(C^k_{2n+1}+C_{2n+1}^{2n+1-k}\right)+C^{2n+1}_{2n+1}=2^{21}\)
\(\sum_{k=0}^{2n+1}C^k_{2n+1}=2^{21}\)
\(\Rightarrow2n+1=21\Rightarrow n=10\)
Số hạng chứa \(x^{26}\) có dạng là:
\(C^k_{10}.\left(\frac{1}{x^4}\right)^k.\left(x^7\right)^{10-k}\Rightarrow-4k+7.\left(10-k\right)=26\)
\(\Rightarrow k=4\)
hệ số của \(x^{26}\) là:
\(C^4_{10}=210\)
ta có : \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}=\sum\limits^{12}_{k=0}C^k_{12}\left(\dfrac{x}{3}\right)^{12-k}.\left(-1\right)^k\left(\dfrac{3}{x}\right)^k\)
\(=\sum\limits^{12}_{k=0}C^k_{12}\left(-1\right)^k\dfrac{\left(x\right)^{12-2k}}{3^{12-2k}}\)
\(\Rightarrow\) để có số hạng chứa \(x^4\) thì \(12-2k=4\Leftrightarrow k=4\)
\(\Rightarrow\) hệ số của số hạng chứa \(x^4\) là : \(\dfrac{C^4_{12}\left(-1\right)^4}{3^4}=\dfrac{55}{9}\)
vậy ............................................................................................................
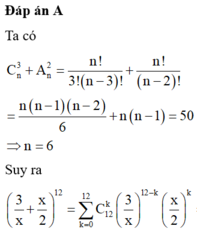
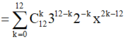
Đáp án B.