Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Xét :
![]()
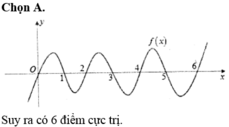
Có nghiệm bội chẵn x = - 1 , x = 1 nên dấu của f’(x) qua hai nghiệm này không đổi dấu => x = 1 và x = - 1 không là cực trị
Có nghiệm bội lẻ x = 2 , x = - 3 2 , nên nó là hai cực trị
Kết luận: Hàm số có hai cực trị.

Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)
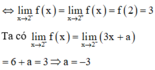

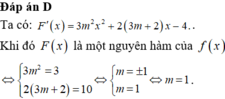

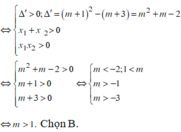

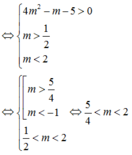
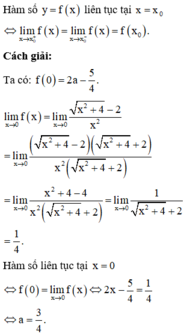

Đáp án là C.
• Txđ: D = ℝ
Với x < 4 ta có f x = a + 2 x 4 ⇒ f x liên tục trên − ∞ ; 4
Với x > 4 ta có : f x = 2 x + 1 − x + 5 x − 4 ⇒ f x = 2 x + 1 − x + 5 x − 4 liên tục trên 4 ; + ∞
• Tại x >4 ta có: f 4 = a + 2
Ta có lim x → 4 − f x = lim x → 4 − a + 2 x 4 = a + 2
lim x → 4 + f x = lim x → 4 + 2 x + 1 − x + 5 x − 4 = lim x → 4 + 1 2 x + 1 + x + 5 = 1 6
Để hàm số f x liên tục trên ℝ khi hàm số f x liên tục tại x = 4 thì
lim x → 4 − f x = lim x → 4 + f x = f 4 ⇔ a + 2 = 1 6 ⇔ a = − 11 6