Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Ta có i = (λD)/a → i1 = 3 mm.
Bề rộng giao thoa L = k 1 i 1 = 24 mm → k 1 = 8. Vậy có 9 vân sáng ứng với ánh sáng có bước sóng λ 1 .
Có 17 vân sáng, 3 vân trùng nằm ở ngoài cùng → số vân sáng ứng với ánh sáng có bước sóng λ 2 là 11 vân. → k 2 = 10.
→ 24 = k 2 i 2 = 10i2 → i 2 = 2,4 mm.
→ λ 2 = a i 2 D = 0 , 2.10 − 3 .2 , 4.10 − 3 = 480 n m .

Chọn C
Trong bề rộng L=2,4 cm =24 mm có 33 vạch sáng có 5 vạch là kết quả trùng nhau của hai hệ vân nên ta có tổng số vân sáng thực sự do hai bức xạ tạo nên là 33+ 5 =38 vân.
Hai trong 5 vạch trùng nhau nằm ở ngoài cùng của trường giao thoa.
Như vậy ta có: 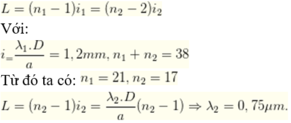

Ta có: \(i_1=3,5/7=0,5mm\)
\(i_2=7,2/8=0,9mm\)
Vân sáng: \(i=\dfrac{\lambda D}{a}\)
Suy ra: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow \lambda_2=\lambda_1.\dfrac{i_2}{i_1}=420.\dfrac{0,9}{0,5}=756nm\)

\(x_s= k\frac{\lambda D}{a}.\)
\(d_2-d_1 = \frac{x_sa}{D}= k\lambda\)
=>\(k= \frac{d_2-d_1}{\lambda}=\frac{1,5.10^{-6}}{\lambda}.(1)\)
Thay các giá trị của bước sóng \(\lambda\)1, \(\lambda\)2,\(\lambda\)3 vào biểu thức (1) làm sao mà ra số nguyên thì đó chính là vân sáng của bước sóng đó.

Số vân sáng quan sát được là
\(N_s = N_{s1}+ N_{s2}-N_{trung nhau} =17.\)
Số vân sáng của \(\lambda_1\) trên trường giao thoa L là
\(N_{s1}= 2.[\frac{L}{2i_1}]+1 = 9.\)
=> \(N_{s2}= N_s-N_{s1}-N_{trung nhau} = 17-9+3=11.\)

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)
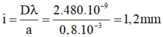
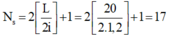

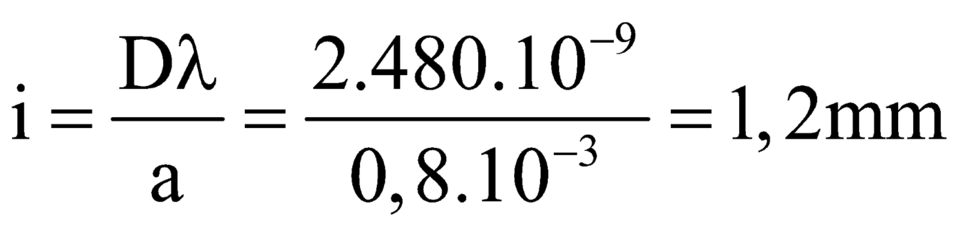
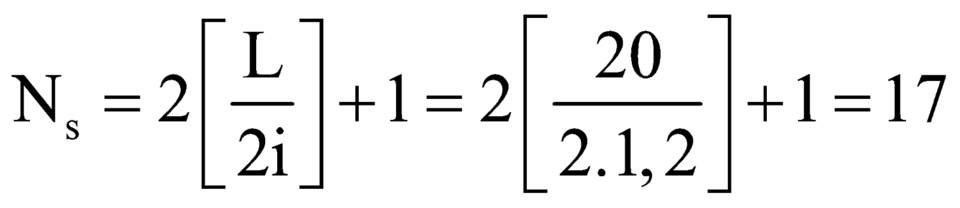
Ta có i = (λD)/a → i1 = 3 mm.
Bề rộng giao thoa L = k1i1 = 24 mm → k1 = 8. Vậy có 9 vân sáng ứng với ánh sáng có bước sóng λ1.
Có 17 vân sáng, 3 vân trùng nằm ở ngoài cùng → số vân sáng ứng với ánh sáng có bước sóng λ2 là 11 vân. → k2 = 10.
→ 24 = k2i2 = 10i2 → i2 = 2,4 mm.
Đáp án C