

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Theo đề, khoảng từ M đến vân sáng trung tâm còn 3 vân sáng nữa: OM = 4i
Khi nhúng vào môi trường chất lỏng có chiết suất n > 1 mà M vẫn là một vân sáng thì số khoảng vân từ M tới vân sáng trung tâm tăng lên do khoảng vân giảm. Vậy, khoảng cách từ M tời vân sáng trung tâm lúc này: OM = 5i’.
\(4\iota=5\iota'\rightarrow4\frac{\text{λ}D}{a}=5\frac{\frac{\text{λ}}{n}D}{a}\rightarrow n=\frac{5}{4}=1,25\)
chọn B

Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Hai khe được chiếu bằng bức xạ có bước sóng 0,6 μmμm. Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm một khoảng 5,4 mm có
A. vân sáng bậc 2
B. vân sáng bậc 4
C. vân sáng bậc 3
D. vân sáng thứ 4

1) i=2mm.
Biết bề rộng miền giao thoa L=3cm=30mm, ta có:
\(\frac{L}{2i}=7,5\) Phần nguyên n=7.
Suy ra số vân sáng: \(N_1=2n+1=15\) vân;
Số vân tối: \(N_2=2\left(n+1\right)=16\) vân.
2) Khi thực hiện thí nghiệm trong môi trường nước, bước sóng ánh sáng là \(\lambda'=\frac{\lambda}{n}\), do đó khoảng vân bây giờ là : \(I'=\lambda'\frac{D}{a}=\frac{i}{n}=1,5mm\)
Ta có: \(\frac{L}{2i'}=10\). Suy ra số vân sáng:\(N'_1=2n+1=21\) vân
Số vân tối : \(N'_2=2n=20\) vân.

Khi đặt thêm bản mỏng trước một trong hai khe thì độ dịch của vân trung tâm là
\(x = \frac{e(n-1)D}{a}\)
Vân trung tâm dời tới vị trí của vân sáng bậc 10 tức là
\(x = x_{s10}= 10.i\)
=> \( \frac{e(n-1)D}{a} = 10.\frac{\lambda D}{a}\)
=> \(e(n-1)=10\lambda\)
=> \(n = \frac{10\lambda }{e}+1=\frac{10.0,5}{10}+1=1,5 \)
Chú ý là giữ nguyên đơn vị của \(\lambda (\mu m)\) và \(e (\mu m)\).
Trong thí nghiệm Y- âng về giao thoa, người ta dùng ánh sáng có bước sóng 0,5 μmμm . Đặt một bản thủy tinh mỏng có độ dầy 10 μmμm vào trước một trong hai khe thì thấy vân sáng trung tâm dời tới vị trí của vân sáng bậc 10. Chiết suất của bản mỏng là
A.1,75.
B.1,45.
C.1,5.
D.1,35.

Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)

Chọn đáp án A
Gọi i và i’ lần lượt là khoảng vân khi thí nghiệm giao thoa thực hiện trong không khí và trong nước
⇒ M N = 10 i → M N 2 i ' = 10 i 2 i ' = 5. i i ' = 5 λ λ ' = 5 c / f v / f = 5 c v = 5 n = 5.4 / 3 = 6 , 67 ( λ , λ ' là bước sóng ánh sáng trong không khí và trong nước)
→ số vân sáng trên đoạn MN khi thí nghiệm giao thoa thực hiện trong nước là 2.6 + 1 = 13.

Gọi i và i’ lần lượt là khoảng vân khi thí nghiệm giao thoa thực hiện trong không khí và trong nước
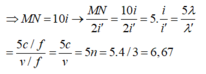
(λ, λ′ là bước sóng ánh sáng trong không khí và trong nước)
→ số vân sáng trên đoạn MN khi thí nghiệm giao thoa thực hiện trong nước là 2.6 + 1 = 13.
Đáp án C

Xây dựng từ phần lý thuyết, hiệu đường đi của ánh sáng từ hai khe đến vân tối thứ \(k+1\) là
\(d_2-d_1 = (k+0,5)\lambda.\)
Áp dụng với \(k+1 = 3\) => \(d_2-d_1 = (2+0,5)\lambda = 2,5 \lambda.\)