Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
\(\iota=\frac{\text{λ}D}{a}\)
\(\rightarrow\iota=\iota_n\rightarrow\frac{\text{λ}D}{a}=\)\(\frac{\frac{\text{λ}}{n}Dn}{a}\rightarrow D_n=n.D=\frac{4}{3}.D\rightarrow D_n-D=\)\(\left(\frac{4}{3}-1\right).D=\frac{1}{3}D\)
\(\iota_n=\frac{\frac{\text{λ}}{n}Dn}{a}\)
Vậy phải rời ra xa thêm D/3

Chọn đáp án C
Khoảng vân trong không khí i = λ D a , khi hệ thống đặt trong nước thì: i ' = λ D a n
Để i = i’ thì D thay đổi đến giá trị D’, ta có: λ D a = λ D ' a n → D ' = n D = 4 D 3
Vậy cần dịch ra xa thêm.

Chọn A
Khoảng vân lúc đầu quan sát được là:
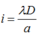
Để lúc sau khoảng vân không đổi thì:
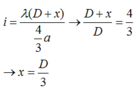
Vì x > 0 nên phải rời màn quan sát ra xa.

1) i=2mm.
Biết bề rộng miền giao thoa L=3cm=30mm, ta có:
\(\frac{L}{2i}=7,5\) Phần nguyên n=7.
Suy ra số vân sáng: \(N_1=2n+1=15\) vân;
Số vân tối: \(N_2=2\left(n+1\right)=16\) vân.
2) Khi thực hiện thí nghiệm trong môi trường nước, bước sóng ánh sáng là \(\lambda'=\frac{\lambda}{n}\), do đó khoảng vân bây giờ là : \(I'=\lambda'\frac{D}{a}=\frac{i}{n}=1,5mm\)
Ta có: \(\frac{L}{2i'}=10\). Suy ra số vân sáng:\(N'_1=2n+1=21\) vân
Số vân tối : \(N'_2=2n=20\) vân.

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

\( i = \frac{\lambda D}{a}= 0,64 mm.\)
Số vân tối quan sát được trên màn là
\(N_t = 2.[\frac{L}{2i}+0,5]=2.9=18.\)

Chọn B
Ta có: i = λD/a
Khi dời màn ra xa thêm 0,6 m thì khoảng vân tăng thêm 0,12 mm tức là:
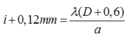
Hay 0,12mm = λ.0,6/a → λ = 0,6μm


Chọn đáp án C