Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ko thể dịch nổi đề câu 1 a;b, chỉ đoán thôi. Còn câu 2 thì thực sự là chẳng hiểu bạn viết cái gì nữa? Chưa bao giờ thấy kí hiệu tích phân đi kèm kiểu đó
Câu 1:
a/ \(\int\frac{2x+4}{x^2+4x-5}dx=\int\frac{d\left(x^2+4x-5\right)}{x^2+4x-5}=ln\left|x^2+4x-5\right|+C\)
b/ \(\int\frac{1}{x.lnx}dx\)
Đặt \(t=lnx\Rightarrow dt=\frac{dx}{x}\)
\(\Rightarrow I=\int\frac{dt}{t}=ln\left|t\right|+C=ln\left|lnx\right|+C\)
c/ \(I=\int x.sin\frac{x}{2}dx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sin\frac{x}{2}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-2cos\frac{x}{2}\end{matrix}\right.\)
\(\Rightarrow I=-2x.cos\frac{x}{2}+2\int cos\frac{x}{2}dx=-2x.cos\frac{x}{2}+4sin\frac{x}{2}+C\)
d/ Đặt \(\left\{{}\begin{matrix}u=ln\left(2x\right)\\dv=x^3dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{2dx}{2x}=\frac{dx}{x}\\v=\frac{1}{4}x^4\end{matrix}\right.\)
\(\Rightarrow I=\frac{1}{4}x^4.ln\left(2x\right)-\frac{1}{4}\int x^3dx=\frac{1}{4}x^4.ln\left(2x\right)-\frac{1}{16}x^4+C\)
a)
Đặt \(\frac{x}{2}=t\Rightarrow 3^{2t}-4=5^t\)
\(\Leftrightarrow 9^t-5^t=4\)
TH1: \(t>1\Rightarrow 9^t-5^t< 4^t\)
\(\Leftrightarrow 9^t< 4^t+5^t\)
\(\Leftrightarrow 1< \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t\) \((*)\)
Ta thấy vì \(\frac{4}{9};\frac{5}{9}<1 \), do đó với \(t>1\Rightarrow \left\{\begin{matrix} \left(\frac{4}{9}\right)^t< \frac{4}{9}\\ \left(\frac{5}{9}\right)^t< \frac{5}{9}\end{matrix}\right.\)
\(\Rightarrow \left(\frac{4}{9}\right)^t+\left(\frac{5}{9}\right)^t< \frac{4}{9}+\frac{5}{9}=1\) (mâu thuẫn với (*))
TH2: \(t<1 \) tương tự TH1 ta cũng suy ra mâu thuẫn
do đó \(t=1\Rightarrow x=2\)
b)
Ta có: \(5^{2x}=3^{2x}+2.5^x+2.3^x\)
\(\Leftrightarrow (5^{2x}-2.5^{x}+1)=3^{2x}+2.3^x+1\)
\(\Leftrightarrow (5^x-1)^2=(3^x+1)^2\)
\(\Leftrightarrow (5^x-3^x-2)(5^x+3^x)=0\)
Dễ thấy \(5^x+3^x>0\forall x\in\mathbb{R}\Rightarrow 5^x-3^x-2=0\)
\(\Leftrightarrow 5^x-3^x=2\)
\(\Leftrightarrow 5^x=3^x+2\)
Đến đây ta đưa về dạng giống hệt phần a, ta thu được nghiệm \(x=1\)
c)
\((2-\sqrt{3})^x+(2+\sqrt{3})^x=4^x\)
\(\Leftrightarrow \left(\frac{2-\sqrt{3}}{4}\right)^x+\left(\frac{2+\sqrt{3}}{4}\right)^x=1\)
TH1: \(x>1\)
Vì \(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1;x> 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x< \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x< \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x<\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
TH2: \(x<1 \)
\(\frac{2+\sqrt{3}}{4};\frac{2-\sqrt{3}}{4}<1; x< 1 \Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x> \frac{2-\sqrt{3}}{4};\left ( \frac{2+\sqrt{3}}{4} \right )^x> \frac{2+\sqrt{3}}{4}\)
\(\Rightarrow \left ( \frac{2-\sqrt{3}}{4} \right )^x+\left ( \frac{2+\sqrt{3}}{4} \right )^x>\frac{2-\sqrt{3}}{4}+\frac{2+\sqrt{3}}{4}=1\) (vô lý)
Do đó \(x=1\)
1.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(y\left(0\right)=5;\) \(y\left(1\right)=3;\) \(y\left(2\right)=7\)
\(\Rightarrow y_{min}=3\)
2.
\(y'=4x^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\end{matrix}\right.\)
\(f\left(-2\right)=-3\) ; \(y\left(0\right)=-3\) ; \(y\left(-\sqrt{2}\right)=-7\) ; \(y\left(1\right)=-6\)
\(\Rightarrow y_{max}=-3\)
3.
\(y'=\frac{\left(2x+3\right)\left(x-1\right)-x^2-3x}{\left(x-1\right)^2}=\frac{x^2-2x-3}{\left(x-1\right)^2}=0\Rightarrow x=-1\)
\(y_{max}=y\left(-1\right)=1\)
4.
\(y'=\frac{2\left(x^2+2\right)-2x\left(2x+1\right)}{\left(x^2+2\right)^2}=\frac{-2x^2-2x+4}{\left(x^2+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(1\right)=1\) ; \(y\left(-2\right)=-\frac{1}{2}\Rightarrow y_{min}+y_{max}=-\frac{1}{2}+1=\frac{1}{2}\)
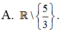
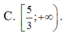
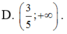
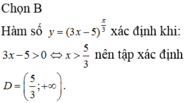
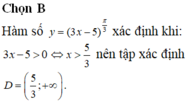
Chọn B
Hàm số y = ( 3 x - 5 ) π 3 xác định khi: 3x - 5 > 0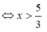
nên tập xác định 