Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(t=3^x,t>0\)
Bất phương trình trở thành :
\(m.t^2+9\left(m-1\right)t+m-1>0\)
\(\Leftrightarrow m\left(t^2+9t+1\right)>9t+1\)
\(\Leftrightarrow m>\frac{9t+1}{t^2+9t+1}\)
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi :
\(m>max_{t>0}\frac{9t+1}{t^2+9t+1}\)
Xét hàm số \(f\left(t\right)=\frac{9t+1}{t^2+9t+1};t>0\)
Ta có : \(f'\left(t\right)=\frac{-9t-2}{\left(t^2+9t+1\right)^2}< 0,t>0\)
đây là hàm nghịch biến suy ra \(f\left(t\right)< f\left(0\right)=1\)
Do đó : \(\frac{9t+1}{t^2+9t+1}< 0,t>0\) nên các giá trị cần tìm là \(m\ge1\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(m-1\right)^2-\left(4m+8\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-6m-7\le0\)
\(\Rightarrow-1\le m\le7\)
\(\Rightarrow m=\left\{-1;0;1;2;3;4;5;6;7\right\}\)

a)
Để \(5x^2-x+m>0\) thì:
\(\Delta< 0\Rightarrow1-20m< 0\Rightarrow m>\dfrac{1}{20}\)
b)
\(mx^2-10x-5< 0\)
Xét \(m=0\) ta có: \(-10x-5< 0\)\(\Leftrightarrow x>\dfrac{1}{2}\) (loại)
Xét \(m\ne0\). Theo định lý về dấu tam thức bậc hai:
\(mx^2-10x-5< 0\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\25+5m< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m< -5\end{matrix}\right.\)\(\Leftrightarrow m< -5\).
Vậy với \(m< -5\) thì \(mx^2-10x-5< 0\).

\(a=4>0\) ; \(-\frac{b}{2a}=\frac{m}{2}\)
TH1: Nếu \(\frac{m}{2}\le-2\Rightarrow\) hàm số đồng biến trên \(\left[-2;0\right]\)
\(\Rightarrow y_{min}=y\left(-2\right)=m^2+6m+16=3\)
\(\Leftrightarrow m^2+6m+13=0\) (vô nghiệm)
TH2: \(\frac{m}{2}\ge0\Rightarrow m\ge0\) hàm số nghịch biến trên \(\left[-2;0\right]\)
\(\Rightarrow y_{min}=y\left(0\right)=m^2-2m=3\)
\(\Rightarrow m^2-2m-3=0\Rightarrow\left[{}\begin{matrix}m=-1\left(l\right)\\m=3\end{matrix}\right.\)
TH3: \(-2< \frac{m}{2}< 0\Rightarrow-4< m< 2\)
\(\Rightarrow y_{min}=y\left(\frac{m}{2}\right)=-2m=3\Rightarrow m=-\frac{3}{2}\)
Vậy \(\sum=-\frac{3}{2}+3=\frac{3}{2}\)
dạ nếu vậy khi làm xong thì có phải thử lại xem giá trị m nào thỏa mãn thì lấy không thì lại ko ạ hay lấy tất ạ

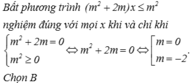
Bất phương trình ( m 2 + 2 m ) x ≤ m 2 nghiệm đúng với mọi x khi và chỉ khi m 2 + 2 m = 0 m 2 ≥ 0 ⇔ m 2 + 2 m = 0 ⇔ [ m = 0 m = - 2 .