Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1 B 0 B B 3 2 120
\(B_1 = B_0 \cos \omega t \)
\(B_2 = B_0 \cos (\omega t - \frac{2\pi}{3} )\)
\(B_3 = B_0 \cos (\omega t + \frac{2\pi}{3} )\)
Giả sử tại t = 0 thì \(B_1 = B_0; B_2 = \frac{B_0}{2} = B_3\)
Tổng hợp 3 véc tơ như hình vẽ \(\overrightarrow {B} = \overrightarrow {B_1} + \overrightarrow {B_2} +\overrightarrow {B_3} \) => \(B = \frac{B_0}{2} + B_0 = 1,5B_0.\)
Véc tơ cảm ứng từ tổng hợp cũng dao động với tần số \(\omega = \omega_0\).
Chọn đáp án.A.
Biên độ của vật dao động cực đại khi xảy ra cộng hưởng ω = ω0
Đáp án C
Đáp án B
+ Tần số góc riêng của hệ :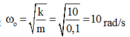
rad/s
+ Xảy ra hiện tượng cộng hưởng khi : 
rad/s khi tang dần tần số góc của ngoại lực cưỡng bức từ 5 rad/s đến 20 rad/s thì tại 
rad/s hệ xảy ra cộng hưởng, biên độ dao động của viên bi lớn nhất
Biên độ của viên bi tang lên cực đại rồi giảm khi thay đổi ω
Khi dung kháng là $100 \Omega$ thì công suất tiêu thụ của đoạn mạch là cực đại bằng 100 W nên
\(\begin{cases} Z_L=Z_{C_1}=100 \Omega \\ P=\dfrac{U^2}{R} =100 W \end{cases}\)
Khi dung kháng là $200 \Omega$ thì điện áp hiệu dụng giữa hai đầu tụ điện là $100\sqrt{2} V$ nên
$U_{C_2}=\dfrac{U.Z_{C_2}}{Z}=\dfrac{200.U}{\sqrt{R^2+(100-200)^2}}=100\sqrt{2}$
$\Rightarrow 2U^2=R^2+100^2$
$\Rightarrow 2.100.R =R^2 +100^2$
$\Rightarrow R=100 \Omega$
Hướng dẫn:
+ Với giá trị tần số nằm trong khoảng hai giá trị cho cùng một biên độ thì biên độ ứng với tần số đó luôn có giá trị lớn hơn A 1 < A 2 .
Đáp án C
Đáp án B
Để biên độ dao động của hệ là lớn nhất (cộng hưởng) thì tần số của ngoại lực phải bằng tần số dao động riêng của hệ → Ω = ω