NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 10 2019
a) \(\sqrt{\frac{25}{81}\cdot\frac{16}{49}\cdot\frac{169}{9}}\\ =\sqrt{\left(\frac{5}{9}\right)^2\cdot\left(\frac{4}{7}\right)^2\cdot\left(\frac{13}{3}\right)^2}\\ =\sqrt{\left(\frac{5}{9}\cdot\frac{4}{7}\cdot\frac{13}{3}\right)^2}\\ =\frac{5}{9}\cdot\frac{4}{7}\cdot\frac{13}{3}\\ =\frac{260}{189}\)
b) \(\sqrt{3\frac{1}{6}\cdot2\frac{14}{25}\cdot2\frac{34}{81}}\\ =\sqrt{\frac{19}{6}\cdot\frac{64}{25}\cdot\frac{196}{81}}\\ =\sqrt{\frac{19}{6}\cdot\left(\frac{8}{5}\right)^2\cdot\left(\frac{14}{9}\right)^2}\\ =\sqrt{\frac{19}{6}\cdot\left(\frac{8}{5}\cdot\frac{14}{9}\right)^2}\\ =\sqrt{\frac{19}{6}\cdot\frac{112}{45}}\\ =\sqrt{\frac{1064}{135}}\)
1 tháng 10 2019
Bổ sung câu b :
\(\sqrt{3\frac{1}{16}.2\frac{14}{25}.2\frac{34}{81}}=\sqrt{\frac{49}{16}.\frac{64}{25}.\frac{196}{81}}=\sqrt{\frac{49}{16}}.\sqrt{\frac{64}{25}}.\sqrt{\frac{196}{81}}=\frac{7}{4}.\frac{8}{5}.\frac{14}{9}=\frac{196}{45}\)
HH
6
13 tháng 8 2020
a) \(\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}\)
=4.5+14:7
=20+2
=22
b) chưa học nhó:))
Y
13 tháng 6 2019
2.+ \(\left(2n+1\right)^2=4n^2+4n+1>4n^2+4n\)
\(\Rightarrow2n+1>\sqrt{4n\left(n+1\right)}=2\sqrt{n\left(n+1\right)}\)
+ \(\frac{1}{\left(2n+1\right)\left(\sqrt{n}+\sqrt{n+1}\right)}=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\left(2n+1\right)\left(\sqrt{n+1}+\sqrt{n}\right)}\)
\(=\frac{\sqrt{n+1}-\sqrt{n}}{2n+1}< \frac{\sqrt{n+1}-\sqrt{n}}{2\sqrt{n\left(n+1\right)}}=\frac{1}{2}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
Do đó : \(A< \frac{1}{2}\left(1-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{48}}-\frac{1}{\sqrt{49}}\right)\)
\(\Rightarrow A< \frac{1}{2}\)
Y
13 tháng 6 2019
1. + \(\frac{1}{\left(n+1\right)\sqrt{n}}=\frac{\left(n+1\right)-n}{\left(n+1\right)\sqrt{n}}=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\left(n+1\right)\sqrt{n}}\)
\(< \frac{\left(\sqrt{n+1}-\sqrt{n}\right)\cdot2\sqrt{n+1}}{\sqrt{n}\left(n+1\right)}=2\cdot\frac{n+1-\sqrt{n\left(n+1\right)}}{\left(n+1\right)\sqrt{n}}=2\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
Do đó : \(A< 2\left(1-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2012}}-\frac{1}{\sqrt{2013}}\right)\)
\(\Rightarrow A< 2\)
Bài 2 tạm thời chưa nghĩ ra :))
7 tháng 10 2020
a) \(\sqrt{49}+\sqrt{25}-4\cdot0,25\)
\(=7+5-1=11\)
b) \(\sqrt{\frac{1}{9}}\cdot\sqrt{0,81}\cdot\sqrt{0,9}\)
\(=\frac{1}{3}\cdot\frac{9}{10}\cdot\frac{3\sqrt{10}}{10}\)
\(=\frac{9\sqrt{10}}{100}\)
c) \(\sqrt{6,4\cdot2400\cdot0,6}\)
\(=\sqrt{64\cdot36\cdot4}\)
\(=8\cdot6\cdot2=96\)
d) \(\sqrt{26^2-24^2}=\sqrt{\left(26-24\right)\left(26+24\right)}\)
\(=\sqrt{2\cdot50}=\sqrt{100}=10\)
DM
31 tháng 3 2017
a) \(\sqrt{16}\cdot\sqrt{25}+\sqrt{196}:\sqrt{49}\)
\(=\sqrt{16\cdot25}+\sqrt{196:49}\)
\(=20+2=22\)
b) \(36:\sqrt{2\cdot3^2\cdot18}-\sqrt{169}\)
\(=36:\sqrt{324}-\sqrt{169}\)
\(=36:18-13=2-13=-11\)
c) \(\sqrt{\sqrt{81}}\)
\(=\sqrt{9}=3\)
d) \(\sqrt{3^2+4^2}\)
\(=\sqrt{9+16}=\sqrt{25}=5\)
7 tháng 6 2017
a) \(\sqrt{16}.\sqrt{25}+\sqrt{196}\div\sqrt{49}\)
\(=4.5+14:7\)
\(=20+2=22\)
b) \(36:\sqrt{2.3^2.18}-\sqrt{169}\)
\(=36:18-13=-11\)
c) \(\sqrt{\sqrt{81}}=\sqrt{9}=3\)
d) \(\sqrt{3^2+4^2}=\sqrt{25}=5\)
S
13 tháng 6 2019
Đặt B là tên biểu thức
Với mọi n thuộc N*, ta có:
\(\frac{1}{\left(n+1\right)\sqrt{n}}=\frac{\sqrt{n}}{n\left(n+1\right)}=\sqrt{n}\left(\frac{1}{n}-\frac{1}{n+1}\right)=\sqrt{n}\left(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{n+1}}\right)\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
\(=\left(1+\frac{\sqrt{n}}{\sqrt{n+1}}\right)\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)< 2\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\) (*)
Áp dụng (*), ta được:
\(B< 2\left(1-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{4}}+...+\frac{1}{\sqrt{2011}}-\frac{1}{\sqrt{2012}}+\frac{1}{\sqrt{2012}}-\frac{1}{\sqrt{2013}}\right)\)
\(=2\left(1-\frac{1}{\sqrt{2013}}\right)=2-\frac{1}{\sqrt{2013}}< 2\)
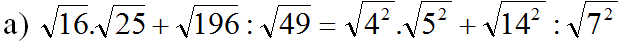
\(=20+\frac{14}{7}=20+2=22\)