Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có các điểm A,B,C có tọa độ lần lượt như sau A(−2;0;0), B(0;3;0), C(0;0;4).
Phương trình mặt phẳng (ABC) theo đoạn chắn là x − 2 + y 3 + z 4 = 1 .
Phương trình tổng quát của mặt phẳng (ABC) là − 6 x + 4 y + 3 z − 12 = 0 .

Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
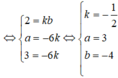

Trong 3 tia ox, oy, oz tia oy nằm giữa 2 tia còn lại vì \(\widehat{xoy}\)<\(\widehat{xoz}\)(30o<110o)
Vì tia oy nằm giữa 2 tia còn lại nên:
\(\widehat{xoy}\)+\(\widehat{yoz}\)=\(\widehat{xoz}\)
30o+\(\widehat{yoz}\)=110o
\(\widehat{yoz}\)=110o-30o=800
Vậy \(\widehat{yoz}\)=80o
Vì tia ot là tia phân giác của \(\widehat{yoz}\)nên:
\(\widehat{toy}\)=\(\widehat{yoz}\)/2=80o/2=40o
Vậy tia\(\widehat{zot}\)=\(\widehat{toy}\)(=40o)
Vì \(\widehat{xoz}\)>\(\widehat{toy}\)(110o<40o) nêm tia oy nằm giữa 2 tia ox và ot:
\(\widehat{xot}\)+\(\widehat{zot}\)=\(\widehat{xoz}\)
\(\widehat{xot}\)+40o=110o
\(\widehat{xot}\) =110o-40o=70o
Vậy \(\widehat{xot}\)=70o

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào



Đáp án C
Ta có: A(-3;0;0), B(0;2;0), C(0;0;4)
Suy ra A B C : x - 3 + y 2 + z 4 = 1 hay 4x - 6y - 3z + 12 = 0
Do vậy mặt phẳng 4x - 6y - 3z + 12 = 0 song song với mặt phẳng (ABC)