Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
![]()
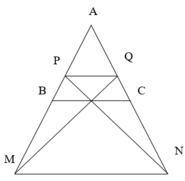
Do ![]() nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho AP=2BP, AQ=2QC. Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d(A,(P))=2.
nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho AP=2BP, AQ=2QC. Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d(A,(P))=2.
TH1: d(A, MQ)=2 nên chỉ có duy nhất 1 mp (P) qua PQ sao cho d(A,(P))=2.
TH2: d(A;MN), d(A;MQ), d(A,NP) đều lớn hơn 2 nên mỗi TH sẽ có 2 mp qua các cạnh MN,MQ,NP sao cho khoảng cách từ A đến nó bằng 2
Vậy có tất cả 7 mp thỏa mãn yêu cầu.

Đáp án B
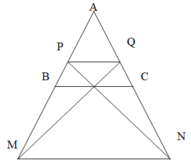
A B = A C = 13 , B C = 4 , d ( A , B C ) = 3 . Do R 1 = 2 R 2 = 2 R 3 nên các khoảng cách từ A đến (P) gấp đôi khoảng cách từ B,C đến (P). gọi M, N lần lượt là điểm đối xứng của A qua B,C. và P,Q là điểm trên canh AB,AC sao cho A P = 2 B P , A Q = 2 Q C . Bài toán quy về tìm các mp (P) chính là các mặt phẳng đi qua MN,MQ,NP,PQ sao cho d ( A , ( P ) ) = 2
TH1: d ( A , P Q ) = 2 nên chỉ có duy nhất 1 mp (P) qua PQ sao cho d ( A , ( P ) ) = 2
TH2: d ( A ; M N ) , d ( A , M Q ) , d ( A ; N P ) đều lớn hơn 2 nên mỗi TH sẽ có 2 mp qua các cạnh MN,MQ,NP sao cho khoảng cách từ A đến nó bằng 2
Vậy có tất cả 7 mp thỏa mãn yêu cầu

Đáp án B.
Gọi phương trình mặt phẳng cần tìm là
P : + b y + c z + d = 0.
Vì d B ; P = d C ; P = 1 suy ra
m p P / / B C hoặc đi qua trung điểm của BC.
Trường hợp 1: với
s u y r a d A ; P = 2 b + c + d b 2 + c 2 = 2
V à d B ; P = − b + c + d b 2 + c 2 = 1 ⇒ 2 b + c + d = 2 − b + c + d − b + c + d = b 2 + c 2 ⇒ 4 b = c + d c + d = 0 − b + c + d = b 2 + c 2
⇔ 3 b = b 2 + c 2 b = b 2 + c 2 ⇔ 8 b 2 = c 2 ⇒ c = ± 2 2 b c = 0 ⇒ d = 0
Suy ra có ba mặt phẳng thỏa mãn.
Trường hợp 2: Mặt phẳng (P) đi qua trùng điểm B C ⇒ P : a x − 1 + b y + 1 + c z − 1 = 0
Do đó d A ; P = 3 b a 2 + b 2 + c 2 = 2 ; d B ; P = 2 a a 2 + b 2 + c 2 = 1
Suy ra 3 b = 4 a 2 a = a 2 + b 2 + c 2 ⇔ 3 b = 4 a 3 a 2 = b 2 + c 2 ( * )
Chọn a =3 suy ra (*)
⇔ b = 4 b 2 + c 2 = 27 ⇔ b = ± 4 c 2 = 11 ⇒ a ; b ; c = 3 ; 4 ; 11 , 3 ; − 4 ; 11 3 ; 4 ; − 11 , 3 ; − 4 ; − 11 .
Vậy có tất cả 7 mặt phẳng thỏa mãn yêu cầu bài toán.

Chọn A
Cách giải:
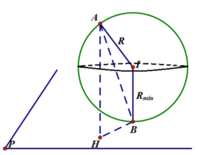
Gọi B là điểm tiếp xúc của mặt cầu (S) và mặt phẳng (P)
=> IB=R
Gọi H là hình chiếu của A xuống (P)



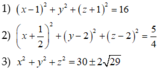
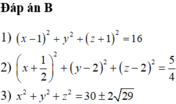



Ta dễ thấy ba điểm A, B, C thuộc mặt phẳng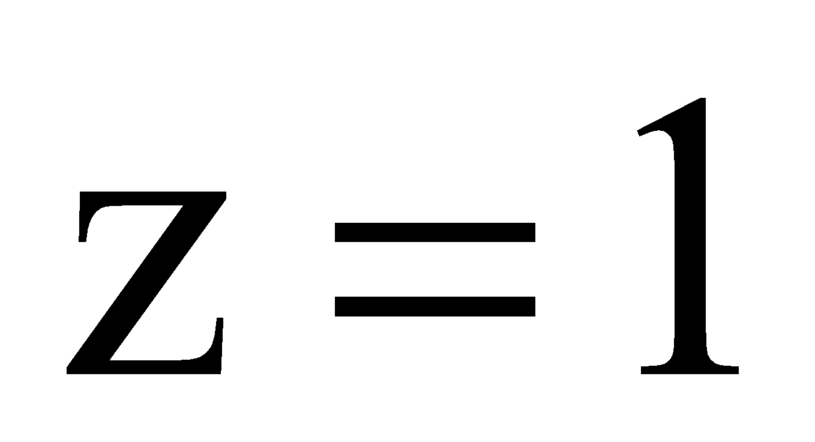 , 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
, 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
1. Cả 3 mặt cầu ở cùng một nửa không gian chia bởi mặt phẳng tiếp xúc. Có 2 mặt phẳng như vậy.
2. Mặt phẳng tiếp xúc chia 2 mặt cầu về một phía và phía còn lại chứa mặt cầu kia. Có 4 mặt phẳng tiếp xúc chia mặt cầu lớn và mặt cầu nhỏ ở cùng một bên. Có một mặt phẳng tiếp xúc chia 2 mặt cầu nhỏ về một bên (ở đây do R + r + d ( A, BC ) nên mới tồn tại 1 mặt phẳng tiếp xúc theo yêu cầu, nếu R + r + d > d ( A, BC ) thì sẽ tồn tại 2 mặt phẳng tiếp xúc)
Đáp án cần chọn là B