Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

Câu 1:
Vì \(\overrightarrow{BA}\uparrow\uparrow\overrightarrow{CD}\) và \(BA=\frac{1}{3}CD\Rightarrow \overrightarrow{BA}=\frac{1}{3}\overrightarrow{CD}\)
Để $B,M,D$ thẳng hàng \(\Leftrightarrow \exists k\in\mathbb{R}|\overrightarrow{BM}=k\overrightarrow{MD}\)
\(\Leftrightarrow \overrightarrow{BA}+\overrightarrow{AM}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}\overrightarrow{CD}+x\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}(\overrightarrow{MC}+\overrightarrow{CD})+(x-\frac{1}{3})\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow \frac{1}{3}\overrightarrow{MD}+(x-\frac{1}{3})\overrightarrow{MC}=k\overrightarrow{MD}\)
\(\Leftrightarrow (x-\frac{1}{3})\overrightarrow{MC}=(k-\frac{1}{3})\overrightarrow{MD}\)
Vì \(\overrightarrow{MC}; \overrightarrow{MD}\) không phải 2 vecto cùng phương nên điều trên chỉ xảy ra khi \(x-\frac{1}{3}=k-\frac{1}{3}=0\Rightarrow x=\frac{1}{3}\)
Bài 2:
Lấy điểm $I(a,b)$ sao cho \(\overrightarrow{IA}-2\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(\Leftrightarrow (1-a, 1-b)-2(4-a, 3-b)+3(2-a, -2-b)=(0,0)\)
\(\Leftrightarrow (-1-2a,-11-2b)=(0,0)\Rightarrow a=-\frac{1}{2}; b=\frac{-11}{2}\)
Vậy \(I(-\frac{1}{2}; -\frac{11}{2})\)
Ta có:
\(|\overrightarrow{MA}-2\overrightarrow{MB}+3\overrightarrow{MC}|=|\overrightarrow{MI}+\overrightarrow{IA}-2(\overrightarrow{MI}+\overrightarrow{IB})+3(\overrightarrow{MI}+\overrightarrow{IC})|\)
\(|2\overrightarrow{MI}+(\overrightarrow{IA}-2\overrightarrow{IB}+3\overrightarrow{IC})|=2|\overrightarrow{MI}|\)
Để \(|\overrightarrow{MA}-2\overrightarrow{MB}+3\overrightarrow{MC}|\) min thì \(|\overrightarrow{MI}|\) min. Điều này xảy ra khi $M$ là hình chiếu của $I$ trên $Ox$
Do đó \(M=(-\frac{1}{2};0)\)
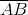 = 3;
= 3; 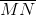 = -5. Từ đây ta có
= -5. Từ đây ta có 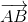 = 3
= 3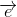 ,
, 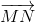 = -5
= -5