Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x = -2 là nghiệm của phương trình: a x 2 + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a x 2 + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình
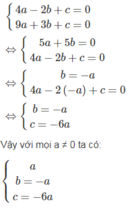

Bài 3 \(\hept{\begin{cases}x+y+xy=2+3\sqrt{2}\\x^2+y^2=6\end{cases}}\)
\(\hept{\begin{cases}\left(x+y\right)+xy=2+3\sqrt{2}\\\left(x+y\right)^2-2xy=6\end{cases}}\)
\(\hept{\begin{cases}S+P=2+3\sqrt{2}\left(1\right)\\S^2-2P=6\left(2\right)\end{cases}}\)
Từ (1)\(\Rightarrow P=2+3\sqrt{2}-S\)Thế P vào (2) rồi giải tiếp nhé. Mình lười lắm ^.^

Giả sử pt: \(x^2+bx+c=0\) có 2 nghiệm phân biệt \(x_1;x_2\) thỏa mãn đề bài.
Theo hệ thức Vi - ét ta có: \(x_1+x_2=-b\) và \(x_1x_2=c\)
Kết hợp với giải thiết ta có: \(x_1=x^2_2+x_2\) và \(b+c=4\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)=4\)
\(\Leftrightarrow x^3_2-2x_2-4=0\)
\(\Leftrightarrow\left(x_2-2\right)\left(x^2_2+2x_2+2\right)=0\)
\(\Leftrightarrow x_2=2\)(Vì: \(x^2_2+2x_2+2=\left(x_2+1\right)^2+1>0\))
Khi đó ta có: \(x_1=4+2=6\Rightarrow b=-8\)và \(c=12\)
Thử lại với \(b=-8;c=12\)ta được pt sau:
\(x^2-8x+12=0\)
\(\Leftrightarrow x_1=6;x_2=2\)(Thỏa mãn yêu cầu bài toán)
Vậy \(\left(b,c\right)=\left(-8;12\right)\) là cặp cần tìm.
x = -2 là nghiệm của phương trình: a x 2 + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a x 2 + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình:
thì phương trình a x 2 + bx + c = 0 có nghiệm x 1 = -2; x 2 = 3
Ví dụ: a = 2, b = -2, c = -12 ta có phương trình:
2 x 2 - 2x - 12 = 0
⇒ x 2 - x - 6 = 0
⇒ (x + 2)(x - 3) = 0
Có nghiệm: x 1 = - 2; x 2 = 3
Có vô số bộ ba a, b, c thỏa mãn yêu cầu bài toán.