Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Khi f = f 1 ta có :
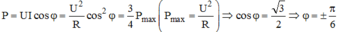
Mà U C = U nên ta có:
Khi f = f 2 thì U L = U . Tương tự ta có:
Từ (1), (2)
mà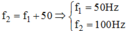 
Khi mạch có cộng hưởng thì: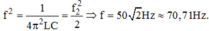 
STUDY TIP
Vận dụng mỗi quan hệ giữa Z L Z C tìm ra f trong mỗi trường hợp và sau đó liên hệ các giả thiết lại với nhau.
trong trường hợp ban đầu
điện áp R cực đại nên tại f1 xảy ra hiện tượng cộng hưởng
\(Z_L=Z_C\)
\(LC=\frac{1}{\omega^2_1}\)
Trong trường hợp sau thì điện áp AM không đổi khi thay đổi R, lúc cố định tần số nghĩa là cảm kháng và dung kháng đều cố định
như vậy thì chỉ có trường hợp duy nhất là Uam bằng với U
Khi đó
\(Z_{LC}=Z_L=Z_C-Z_L\)
\(Z_C=2Z_L\)
\(LC=\frac{1}{2\omega^2_2}\)
Suy ra
\(\omega^2_1=2\omega^2_2\)
\(f_1=\sqrt{2}f_2\)
Đáp án D
Dùng phương pháp chuẩn hóa:
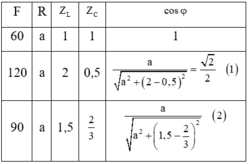
Giải (1) ta được: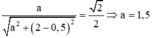 
Thay a=1,5 vào (2) ta có:
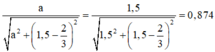
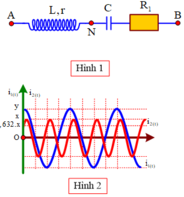
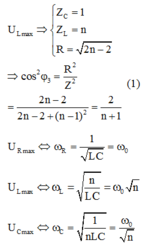
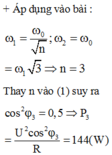
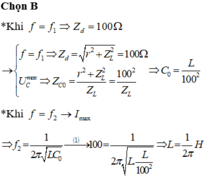
Đáp án B
+ Khi f = f 1 = f C → điện áp hiệu dụng trên tụ cực đại
Công suất tiêu thụ của toàn mạch P = P max cos 2 φ = 0 , 75 P max ⇒ cos 2 φ = 2 1 + n = n = 7 6 .
+ Khi f = f 2 = f 1 + 100 = f L
điện áp hiệu dụng trên cuộn cảm cực đại:
n = f L f C = f 1 + 100 f 1 = 7 6 ⇒ f 1 = 150 H z . Ghi chú: Với bài toán tần số góc biến thiên để điện áp hiệu dụng trên các phần tử cực đại, ta có thể áp dụng kết quả chuẩn hóa sau:
Ta để ý rằng khi tăng dần ω thì thứ tự cực đại của các điện áp là
ω C = X L → ω L = 1 L C → ω L = 1 C X
ω L ω C = ω R 2
Để đơn giản cho biểu thức ta tiến hành chuẩn hóa X = 1 và đặt n = ω L ω C = L C .
+ Khi U C max thì ω C = X L ⇒ Z L = X = 1 , n = L C = Z L Z C ⇒ Z C = n
khi đó U C max = U 1 - n - 2 cos φ = 2 n + 1
+ Khi U L max thì ω L = 1 C X ⇒ Z C = X = 1 , n = L C = Z L Z C ⇒ Z L = n
khi đó U L max = U 1 - n - 2 cos φ = 2 n + 1