Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b

Vì \(\sqrt{x}\ge0\Rightarrow0\le\sqrt{x}< 3\)
\(\Rightarrow0\le x< 9\Rightarrow x\in\left\{0;1;2;...;8\right\}\)
\(b,x^2=5\)
\(\Rightarrow\sqrt{x^2}=\pm\sqrt{5}\)
\(\Rightarrow x=\pm\sqrt{5}\)
c, Ta có:\(x\ne0\left(\sqrt{x}\ge0\forall x\right)\)
\(\Rightarrow\sqrt{0}\le\sqrt{x}< \sqrt{2}\)
\(\Rightarrow0\le x< 4\)
\(\Rightarrow x\in\left\{0;1;2;3\right\}\)

a)\(\frac{3x-2}{5}\ge\frac{x}{2}+0,8\) va \(1-\frac{2x-5}{6}>\frac{3-x}{4}\)
\(\cdot\frac{3x-2}{5}\ge\frac{x}{2}+0,8\)
\(=\frac{2\left(3x-2\right)}{10}\ge\frac{5x}{10}+\frac{8}{10}\)
\(\Rightarrow2\left(3x-2\right)\ge5x+8\)
\(=6x-4\ge5x+8\)
\(=6x-5x\ge8+4\)
\(x\ge12\)(1)
\(\cdot1-\frac{2x-5}{6}>\frac{3-x}{4}\)
\(=\frac{12}{12}-\frac{2\left(2x-5\right)}{12}>\frac{3\left(3-x\right)}{12}\)
\(\Rightarrow12-2\left(2x-5\right)>3\left(3-x\right)\)
\(=12-4x+10>9-3x\)
\(=-4x+3x>9-12-10\)
\(=-x>-13\)
\(=x< 13\) (2)
Từ (1) và (2) => \(13>x\ge12\)=> x=12

1.
TH1: nếu trong 3 số có ít nhất 1 số bằng 0, không mất tính tổng quát, giả sử đó là a \(\Rightarrow b+c=0\Rightarrow b=-c\)
\(\Rightarrow a^{2011}+b^{2011}+c^{2011}=0+b^{2011}+\left(-b\right)^{2011}=0< 2\) (thỏa mãn)
TH2: nếu cả 3 số đều khác 0 \(\Rightarrow\) trong 3 số tồn tại ít nhất 1 số âm, giả sử đó là a
\(\Rightarrow a^{2011}< 0\)
Mặt khác do \(-1\le b\le1\Rightarrow b^{2011}\le\left|b\right|^{2011}\le1\)
Tương tự: \(c^{2011}\le1\)
\(\Rightarrow a^{2011}+b^{2011}+c^{2011}\le a^{2011}+1+1\le a^{2011}+2< 2\) (đpcm)
2.
\(\Leftrightarrow\frac{2\left(x-5\right)+10}{x-5}-\frac{3}{x-1}< 2\)
\(\Leftrightarrow2+\frac{10}{x-5}-\frac{3}{x-1}< 2\Leftrightarrow\frac{10}{x-5}-\frac{3}{x-1}< 0\)
\(\Leftrightarrow\frac{10x-10-3x+15}{\left(x-5\right)\left(x-1\right)}< 0\Leftrightarrow\frac{7x+5}{\left(x-5\right)\left(x-1\right)}< 0\)
\(\Rightarrow\left[{}\begin{matrix}x< -\frac{5}{7}\\1< x< 5\end{matrix}\right.\)

Bài 1: Giả sử \(C\ge0\)
Ta có:
\(C=b^3-a^3-6b^2-a^2+9b\ge0\)
\(\Leftrightarrow\left(b^3-6b^2+9b\right)-\left(a^3+a^2\right)\ge0\Leftrightarrow b\left(b^2-6b+9\right)-a^2\left(a+1\right)\ge0\)
\(\Leftrightarrow b\left(b-3\right)^2-a^2\left(a+1\right)\ge0\)
Mà \(a+b=3\Rightarrow b=3-a\)
\(\Rightarrow C=\left(3-a\right)\left(3-a-3\right)^2-a^2\left(a+1\right)\ge0\Leftrightarrow a^2\left(3-a\right)-a^2\left(a+1\right)=a^2\left(2-2a\right)\ge0\)
Ta có: \(a^2\ge0;a\le0\Rightarrow2a\le0\Rightarrow-2a\ge0\Rightarrow2-2a\ge2\Rightarrow C\ge0\)(luôn đúng)
Bài 2: để suy nghĩ đã á

Ta có
a) a - 5 \(\ge\) b - 5 ↔ a - 5 + 5 \(\geq\) b - 5 + 5 ↔ a \(\ge\) b
b) 15 + a \(\le\) 15 + b ↔ 15 + a - 15 \(\le\) 15 + b - 15 ↔ a \(\leq\) b

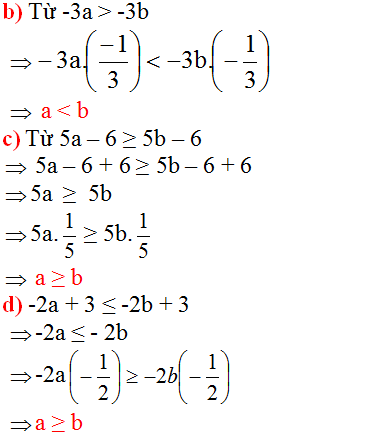

Ta có: x < 5 ⇔ (a – b)x < 5(a – b)
⇒ a – b > 0 ⇔ a > b