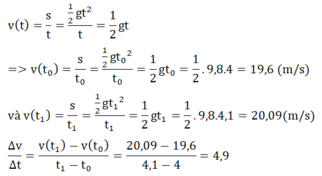Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49 m/s.

a, Phương trình vận tốc v(t) = s'(t) = gt
Vận tốc tức thời tại thời điểm t0 = 4(s) là: \(v\left(4\right)=39,2\left(m/s\right)\)
Vận tốc tức thời tại thời điểm t0 = 4,1s) là: \(v\left(4,1\right)=40,18\left(m/s\right)\)
b, Tỉ số \(\dfrac{\Delta v}{\Delta t}=\dfrac{40,18-39,2}{4,1-4}=9,8\)

Phương trình vận tốc của vật là: v(t) = s'(t) = gt
Phương trình gia tốc của vật là: a(t) = v'(t) = g = 9,8 m/s2
a, Vận tốc tại thời điểm t0 = 2(s) = \(9,8\cdot2=19,6\left(m/s\right)\)
b, Gia tốc của vật tại mọi thời điểm là a = g = 9,8 m/s2

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s

a) Vận tốc trung bình trong khoảng thời gian từ t đến t + Δt là:

b) Vận tốc tức thời tại thời điểm t = 5s chính là vận tốc trung bình trong khoảng thời gian (t; t + Δt) khi Δt → 0 là :
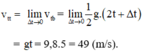

Câu 1:
\(\left(2x+1\right)\left(x^2-2x+3\right)=2x^3-4x^2+6x+x^2-2x+3\)
\(=2x^3-3x^2+4x+3\)
\(\Rightarrow\left[\left(2x+1\right)\left(x^2-2x+3\right)\right]'=6x^2-6x+4\) \(\Rightarrow a+b+c=6-6+4=4\)
Câu 2:
\(v\left(t\right)=s'\left(t\right)=-t^3+9t^2-2\)
\(a\left(t\right)=v'\left(t\right)=-3t^2+18t\)
\(a'\left(t\right)=-6t+18=0\Rightarrow t=3\)
\(\Rightarrow\) vật đạt gia tốc lớn nhất sau 3s kể từ khi chuyển động
Câu 3:
\(y'=x^2-6x-9\)
Gọi tiếp tuyến d' tại \(M\left(x_0;y_0\right)\) có pt \(y=\left(x_0^2-6x_0-9\right)\left(x-x_0\right)+y_0\)
Do \(d//d'\Rightarrow x_0^2-6x_0-9=3\Rightarrow x_0^2-6x_0-12=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=3+\sqrt{21}\\x_0=3-\sqrt{21}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y_0=...\\y_0=...\end{matrix}\right.\) \(\Rightarrow\) pttt
Có vẻ bạn chép sai đề, tiếp tuyến quá xấu
Câu 4:
S A B C D I
Ta có: \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(BD\perp AC\) (tính chất hình thoi)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SI\)
b/ \(\left(SBD\right)\cap\left(ABCD\right)=BD\); mà \(\left(SAC\right)\perp BD\)
\(\Rightarrow\widehat{SIA}\) là góc giữa (SBD) và (ABCD)
Đặt \(AB=x\); do \(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều \(\Rightarrow AC=x\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=x.1=x\)
\(AI=\frac{1}{2}AC=\frac{x}{2}\Rightarrow tan\widehat{SIA}=\frac{SA}{AI}=\frac{x}{\frac{x}{2}}=2\)
\(\Rightarrow\widehat{SIA}\approx63^026'\)

a) Vận tốc tức thời \(v\left( t \right)\) tại thời điểm \(t\) là: \(v\left( t \right) = s'\left( t \right) = 6{t^2} + 4\).
b) Gia tốc \(a\left( t \right)\) của chuyển động tại thời điểm \(t\) là: \(a\left( t \right) = v'\left( t \right) = 12t\).
Gia tốc của chuyển động tại thời điểm \(t = 2\) là: \(a\left( 2 \right) = 12.2 = 24\).

a, Phương trình vận tốc là: v(t) = \(3t^2-6t+8\)
Phương trình gia tốc là: a(t) = \(6t-6\)
Thay t = 3 vào phương trình, ta được:
s = \(3^3-3\cdot3^3+8\cdot3+1=25\left(m\right)\)
\(v=3\cdot3^2-6\cdot3+8=17\left(m/s\right)\\ s=6\cdot3-6=12\left(m/s^2\right)\)
b, Theo đề bài, ta có:
\(t^3-3t^2+8t+1=7\\ \Leftrightarrow t^3-3t^2+8t-6=0\\ \Leftrightarrow\left(t-1\right)\left(t^2-2t+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=1\\t^2-2t+6=0\left(vô.nghiệm\right)\end{matrix}\right.\)
Khi t = 1(s), chất điểm đi được 7m
\(v=3\cdot1^2-6\cdot1+8=5\left(m/s\right)\\ a=6\cdot1-6=0\left(m/s^2\right)\)

\(a,v\left(t\right)=s'\left(t\right)=3t^2-12t-9\)
Vận tốc của vật tại thời điểm t = 2s là: \(v\left(2\right)=3\cdot2^2-12\cdot2+9=-3\left(m/s\right)\)
Vận tốc của vật tại thời điểm t = 4s là: \(v\left(4\right)=3\cdot4^2-12\cdot4+9=9\left(m/s\right)\)
b, Khi vật đứng yên, ta có:
\(v\left(t\right)=0\Leftrightarrow3t^2-12t+9=0\Leftrightarrow\left[{}\begin{matrix}t=3\\t=1\end{matrix}\right.\)
c, Ta có \(a\left(t\right)=s"\left(t\right)=6t-12\)
Gia tốc của vật tại thời điểm t = 4s là \(a\left(4\right)=6\cdot4-12=12\left(m/s^2\right)\)
d, Ta có: Khi t = 1s hoặc t = 3s thì vật đứng yên.
Như vậy, ta cần tính riêng quãng đường vật đi được từng khoảng thời gian \(\left[0;1\right],\left[1;3\right],\left[3;5\right]\)
Từ thời điểm t = 0s đến thời điểm t = 1s, vật đi được quãng đường là:
\(\left|f\left(1\right)-f\left(0\right)\right|=\left|4-0\right|=4m\)
Từ thời điểm t = 1s đến thời điểm t = 3s, vật đi được quãng đường là:
\(\left|f\left(3\right)-f\left(1\right)\right|=\left|0-4\right|=4m\)
Từ thời điểm t = 3s đến thời điểm t = 5s, vật đi được quãng đường là:
\(\left|f\left(5\right)-f\left(3\right)\right|=\left|20-0\right|=20m\)
Tổng quãng đường vật đi được trong 5s đầu tiên là: 28m
e,Xét \(a\left(t\right)=0\Leftrightarrow t=2\)
Với \(t\in[0;2)\) thì gia tốc âm, tức là vật giảm tốc.
Với \(t\in(2;5]\) thì gia tốc dương, tức là vật tăng tốc.