Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4 cm = 40 mm; 5 cm = 50 mm; 6 cm = 60 mm
Ta có: \(\frac{40}{8}=\frac{50}{10}=\frac{60}{12}\)
=> Tam giác ABC đồng dạng tam giác A'B'C'

a) Hai tam giác đồng dạng với nhau vì \(\dfrac{40}{8}=\dfrac{50}{10}=\dfrac{60}{12}\) (cùng bằng 5)
b) Hai tam giác không đồng dạng với nhau vì \(\dfrac{3}{9}\ne\dfrac{4}{15}\)
c) Hai tam giác đồng dạng với nhau vì \(\dfrac{1}{2}=\dfrac{1}{2}=\dfrac{0,5}{1}\)

a) Ta có: \(\frac{4}{8}=\frac{5}{10}=\frac{6}{12}\left(=\frac{1}{2}\right)\)
hay \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}\)
\(\Rightarrow\)\(\Delta A'B'C'~\Delta ABC\)
b) \(\Delta A'B'C'~\Delta ABC\)
\(\Rightarrow\)\(\frac{P_{A'B'C'}}{P_{ABC}}=\frac{A'B'}{AB}=\frac{8}{4}=2\)
Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !
Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber

Lời giải:
a) Ta thấy:
$\frac{4}{8}=\frac{5}{10}=\frac{6}{12}$ nên 2 tam giác đồng dạng theo TH c.c.c
b) Pitago: $A'C'=\sqrt{B'C'^2-A'B'^2}=\sqrt{16^2-9^2}=5\sqrt{7}$
Xét tam giác $ABC$ và $A'B'C'$ có:
$\widehat{A}=\widehat{A'}=90^0$
$\frac{AB}{AC}\neq \frac{A'B'}{A'C'}$
Do đó 2 tam giác không đồng dạng

Ta có: 3/9 = 6/18 ≠ 4/15 . Vậy hai tam giác đó không đồng dạng.
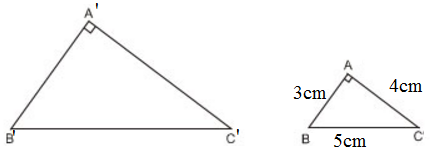

Ta có: 4/8 = 5/10 = 6/12 .Vậy hai tam giác đó đồng dạng