Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách giải:
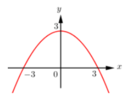
Gắn hệ trục tọa độ như hình vẽ.
Gọi phương trình parabol là: y = a x 2 + b x + c


Bài 1 :
giải :
Chiều rộng là
150:3x2=100[m]
Diện tích là
150x100=15000[m2]
thu hoạch được số thóc là
15000:100=150[kg]
đáp số : 150kg thóc
Bài 2:
giải
a) Thể tích bể là 4x3x2,5=30(m3)
đổi 30m3=30000 lít
Số nước có trong bể= 30000x80%=24000(l)
b) đổi 24000l=24m3
mức nc trong bể cao 24:4:3=2(m)

Câu 1: Gập mảnh vải thành 4 phần bằng nhau rồi cắt đi một phần.

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

n6 - n4 + 2n3 + 2n2
= n2 . (n4 - n2 + 2n +2)
= n2 . [n2(n - 1)(n + 1) + 2(n + 1)]
= n2 . [(n + 1)(n3 - n2 + 2)]
= n2 . (n + 1) . [(n3 + 1) - (n2 - 1)]
= n2. (n + 1)2 . (n2 - 2n + 2)
Với n ∈ N, n > 1 thì n2 - 2n + 2 = (n - 1)2 + 1 > (n - 1)2
Và n2 - 2n + 2 = n2 - 2(n - 1) < n2
Vậy (n - 1)2 < n2 - 2n + 2 < n2
=> n2 - 2n + 2 không phải là một số chính phương.

Người thợ đó gấp đôi mảnh vải chia thành 2 phần, sau đó tiếp tục gấp đôi manh vải của mỗi mãnh vai trên chia thành 4 phần . Bây giờ người thợ đó cắt \(\dfrac{3}{4}\) mảnh vải dựa theo 4 phần đã chia thì ta có 1 mảnh vải có diện tích 1m\(^2\).

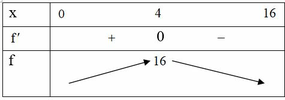

Chọn B.
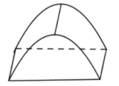
Phương pháp: Sử dụng tích phân.
Cách giải: Chọn hệ trục tọa độ như hình sao cho mặt trước của lều là mặt (Oxy), mặt đáy lều là mặt (Oyz).