Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

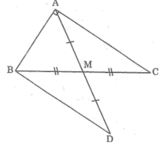
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.

tự kẻ hình nha
a) xét tam giác BMD và tam giác CMA có
AM=MD(gt)
BM=CM(gt)
AMC=BMD( đối đỉnh)
=> tam giác BMD= tam giác CMA(cgc)
=> BDM=MAC( hai góc tương ứng)
mà BDM so le trong với MAC=> AC//BD, BA vuông góc với AC=> BA vuông góc với BD=> ABD=90 độ
b) từ tam giác BMD= tam giác CMA=> BD=AC( hai cạnh tương ứng)
xét tam giác ABC và tam giác BAD có
BD=AC(cmt)
AB chung
BAC=ABD(=90 độ)
=> tam giác ABC= tam giác BAD(cgc)
c) từ tam giác ABC= tam giác BAD => AD=BC( hai cạnh tương ứng)
mà AM=MD=> M là trung điểm của AD
và M là trung điểm của BC=> AM=MD=BM=CM
=> 2AM=BM+CM
=> 2AM=BC
=> AM=1/2BC

A B C M D
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.

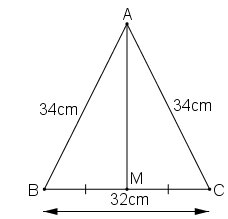
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

2:
a: Xét ΔABC có BM,CN là trung tuyến và G là giao của BM,CN
nên G là trọng tâm
=>BG=2GM và CG=2GN
=>BG=GE và CG=GF
=>G là trung điểm chung của BE và CF
=>BCEF là hình bình hành
=>BC=EF
b: Xét ΔFAE và ΔBGC có
FA=BG
AE=GC
FE=BC
=>ΔFAE=ΔBGC

tu ve hinh :
a, xet tamgiac MBA va tamgiac MDC co :
goc BMA = goc DMC (doi dinh)
BM = CM do M la trung diem cua BC (GT)
MA = MD (GT)
=> tamgiac MBA = tamgiac MDC (c - g - c)
=> AB = DC (dn)
tamgiac MBA = tamgiac MDC => goc CDM = goc MAB ma 2 goc nay slt
=> AB // CD (dh)
b, co tamgiac ABC vuong tai A => AB | AC (dn) ; AB // DC (cau a)
=> AC | DC (dl) => tamgiac ACD vuong tai C (dn)
tamgiac MBA = tamgiac MDC => AB = CD (dn)
goc BAC = goc DCA = 90o do tamgiac ABC vuong tai A va tamgiac DCA vuong tai C
xet tamgiac ACB va tamgiac CAD co AC chung
=> tamgiac ACB = tamgiac CAD (2cgv)
=> BC = AD (dn)
M la trung diem cua BC => M la trung diem cua AD => AM = AD/2 (tc)
=> AM = BC/2

Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.