Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64

Chọn C
Ta có:
∑
k
=
0
2020
C
2020
k
-
∑
k
=
0
2019
C
2019
k
![]()
![]()
Vì một đồng xu có hai mặt nên khi gieo 2019 đồng xu phân biệt ta có 2 2019 kết quả có thể xảy ra của phép thử. Vậy số
phần tử của không gian mẫu là n( Ω ) = 2 2019 .

b. Biến cố C: “ Có ít nhất hai đồng tiền xuất hiện mặt ngửa” tức là có thể có hai hoặc ba đồng tiền xuất hiện mặt ngửa. Vì vậy chọn phương án B

Lời giải:
Xác suất để xu 1 ngửa: $\frac{1}{2}$
Xác suất để xu 2 ngửa: $\frac{1}{2}$
Xác suất để xu 3 ngửa: $\frac{1}{2}$
Xác suất để 3 mặt cùng ngửa: $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}$

Đáp án B
Phương pháp: Nhân xác suất.
Cách giải: Gọi số lần Amelia tung đồng xu là n , ( n ∈ N * ) => Số lần Blaine tung là n - 1
Amelia thắng ở lần tung thứ n của mình nên n - 1 lượt đầu Amelia tung mặt sấp, lần thứ n tung mặt ngửa, còn toàn bộ n - 1 lượt của Blaine đều sấp. Khi đó:
Xác suất Amelia thắng ở lần tung thứ n:
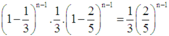
Xác suất Amelia thắng :
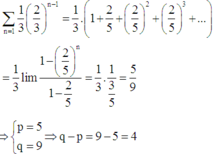

a) Ω = {S1, S2, S3, S4, S5, N1, N2, N3, N4, N5}
b)
A = {S2, S4, S6};
B = {N1, N3, N5}.


Chọn A
Ghi nhớ:
-Phép thử “gieo hai đồng tiền phân biệt” thì hai kết quả SN, NS của phép thử là khác nhau.
-Phép thử “gieo n đồng xu phân biệt” thì không gian mẫu có 2 n phần tử, với n ∈ ℕ * .