Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

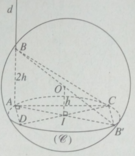
Diện tích tam giác BCD bằng:
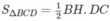
Diện tích này lớn nhất khi AI // CD.

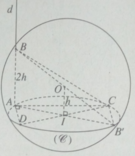
Tam giác ADC vuông tại A nên AD 2 = DC 2 - AC 2 (1)
Tam giác ABC vuông tại A nên BC 2 = AC 2 + AB 2 (2)
Từ (1) và (2) ta suy ra AD 2 + BC 2 = DC 2 + AB 2 (3)
Ta lại có:
AC 2 = DC 2 - AD 2 và BD 2 = AD 2 + AB 2 (4)
DC 2 = 4 r 2 - h 2 , AB 2 = 4 h 2 (5)
Từ (4) và (5) ta có:
AC 2 + BD 2 = DC 2 + AB 2 = 4 r 2 - h 2 + 4 h 2 = 4 r 2 (6)
Từ (3) và (6) ta có: AD 2 + BC 2 = AC 2 + BD 2 (không đổi)

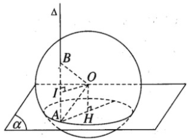
Mặt phẳng (ABO) qua tâm O của hình cầu nên cắt mặt cầu theo đường tròn lớn qua A và B. Gọi I là trung điểm của đoạn AB ta có OI ⊥ AB. Vì AB // OH nên AIOH là hình chữ nhật.
Do đó
![]()
Vậy AB = 2AI = r
Chú ý: Có thể nhận xét rằng tam giác OAB cân tại O (OA = OB) và có góc ∠ OAB = 60 ° nên OAB là tam giác đều và suy ra AB = OA = OB = r.

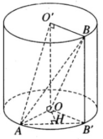
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là 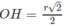










Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).