Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C D M N H K
Thế tích của khối chóp S.CDNM :
\(S_{CDNM}=S_{ABCD}-S_{AMN}-SBC\)
\(=AB^2-\frac{1}{2}AM.AN-\frac{1}{2}BC.BM\)
\(=a^2-\frac{a^2}{8}-\frac{a^2}{4}=\frac{5a^2}{8}\)
Vậy \(V_{SCDNM}=\frac{1}{3}S_{CDNM.SH}=\frac{5\sqrt{3}a^2}{24}\)
Khoảng cách giữa 2 đường thẳng DM và SC
\(\Delta ADM=\Delta DCN\Rightarrow\widehat{ADM}=\widehat{DCN}\Rightarrow DM\perp CN\)
Kết hợp với điều kiện :
\(DM\perp SH\Rightarrow DM\perp\left(SHC\right)\)
Hạ \(HK\perp SC\left(K\in SC\right)\Rightarrow HK\)là đoạn vuông góc chung của DM và SC
Do đó :
\(d\left(DM,SC\right)=HK\)
Ta có :
\(\begin{cases}HC=\frac{CD^2}{CN}=\frac{2a}{\sqrt{5}}\\HK=\frac{SH.HC}{\sqrt{SH^2+HC^2}}=\frac{2\sqrt{3}a}{\sqrt{19}}\end{cases}\)
\(\Rightarrow d\left(DM,SC\right)=\frac{2\sqrt{3}a}{\sqrt{19}}\)
cậu ơi, hướng dẫn giúp tớ bài tương tự này với: cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, góc giữa SD và mặt phẳng ABCD là 45 độ, SA vuông góc (ABCD). M là trung điểm BC. Tính khoảng cách DM và SC
cảm ơn c nhiều nhiều.

S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

B A D C B1 C1 A1 F K E H
Gọi (\(\alpha\)) là mặt phẳng chứa DE và song song với \(A_1F\) thì khoảng cách cần tính bằng khoảng cách từ F đến ( \(\alpha\))
Theo giả thiết suy ra lăng trụ đã cho là lăng trụ đứng có đáy là tam giác đều cạnh a
Gọi K là trung điểm của \(FC_1\) thì \(EK\)//\(A_1F\)//AD, suy ra (\(\alpha\)) \(\equiv\left(ADKE\right)\)
Ta có \(A_1F\perp B_1C_1\Rightarrow A_1F\perp\left(BCC_1B_1\right)\) \(\Rightarrow EK\perp\left(BCC_1B_1\right)\)
Gọi H là hình chiếu vuông góc của F lên đường thẳng DK thì \(FH\perp\left(ADKE\right)\) suy ra FH là khoảng cách cần tính
Trong tam giác vuông DKF, ta có :
\(\frac{1}{FH^2}=\frac{1}{FD^2}+\frac{1}{FK^2}=\frac{1}{\left(\frac{a}{4}\right)^2}\Rightarrow FH=\frac{a}{\sqrt{17}}\)

Bài 14:
Vecto chỉ phương của đường thẳng $d$ là: $\overrightarrow{u_d}=(1; -1; 2)$
Mp $(P)$ vuông góc với $d$ nên nhận $\overrightarrow{u_d}$ là vecto pháp tuyến
Do đó PTMP $(P)$ là:
$1(x-x_M)-1(y-y_M)+2(z-z_M)=0$
$\Leftrightarrow x-y+2z=0$
Đáp án A
Bài 13:
Khi quay tam giác đều ABC quanh cạnh AB thì ta thu được một khối hình là hợp của 2 hình nón (ngược chiều nhau) có cùng bán kính đáy $r$ là đường cao của tam giác đều, tức là $r=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$ và đường cao là $h=\frac{AB}{2}=\frac{1}{2}$
Thể tích 1 hình nón: $V_n=\frac{1}{3}\pi r^2h=\frac{\pi}{8}$
Do đó thể tích của khối hình khi quay tam giác đều ABC quanh AB là: $2V_n=\frac{\pi}{4}$

3.
\(r=\frac{h}{2}=3\Rightarrow V=\frac{1}{3}h.\pi r^2=\frac{1}{3}.6.\pi.3^2=18\pi\)
4.
\(z=-3+4i\Rightarrow iz=i\left(-3+4i\right)=-4-3i\)
Điểm biểu diễn là \(N\left(-4;-3\right)\)
5.
d nhận 1vtcp là (2;-1;3) nên (P) cũng nhận (2;-1;3) là 1 vtpt
1.
Xếp 8 bạn theo thứ tự bất kì \(\Rightarrow\) có \(8!\) cách
Xếp Việt Nam cạnh nhau có 2 cách
Coi 2 bạn Việt Nam là 1 người, xếp 7 người vào 7 ghế có \(7!\) cách
\(\Rightarrow\) Có \(7!.2\) cách xếp 2 bạn Việt Nam ngồi cạnh nhau
Xác suất: \(P=\frac{7!.2}{8!}=\frac{1}{4}\)
2.
Chắc là tứ diện đều?
Gọi O là tâm đáy \(\Rightarrow AO=\frac{a\sqrt{6}}{3}\) . Qua C kẻ đường thẳng song song BM cắt BD kéo dài tại E
\(\Rightarrow BM//\left(ACE\right)\Rightarrow d\left(BM;AC\right)=d\left(BM\left(ACE\right)\right)=d\left(O;\left(ACE\right)\right)\)
Từ O kẻ \(OH\perp CE\Rightarrow OH=CM=\frac{CD}{2}=\frac{a}{2}\)
Từ O kẻ \(OK\perp AH\Rightarrow OK\perp\left(ACE\right)\Rightarrow OK=d\left(O;\left(ACE\right)\right)\)
\(\frac{1}{OK^2}=\frac{1}{OA^2}+\frac{1}{OH^2}\Rightarrow OK=\frac{OA.OH}{\sqrt{OA^2+OH^2}}=\frac{a\sqrt{22}}{11}\)



Ta chọn hệ trục tọa độ như sau: B 1 là gốc tọa độ, B 1 A 1 → = i → , B 1 C 1 → = j → , B 1 B → = k → . Trong hệ trục vừa chọn, ta có B 1 (0; 0; 0), B(0; 0; 1), A 1 (1; 0; 0), D 1 (1; 1; 0), C(0; 1; 1), D(1; 1; 1), C 1 (0; 1; 0).
Suy ra M(0; 0; 1/2), P(1; 1/2; 0), N(1/2; 1; 1)
Ta có MP → = (1; 1/2; −1/2); C 1 N → = (1/2; 0; 1)
Gọi ( α ) là mặt phẳng chứa C 1 N và song song với MP. ( α ) có vecto pháp tuyến là n → = (1/2; −5/4; −14) hay n ' → = (2; −5; −1)
Phương trình của ( α ) là 2x – 5(y – 1) – z = 0 hay 2x – 5y – z + 5 = 0
Ta có:
d(MP, C 1 N) = d(M,( α ))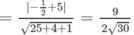
Ta có:
Vậy ∠ (MP, C 1 N) = 90 ° .