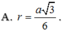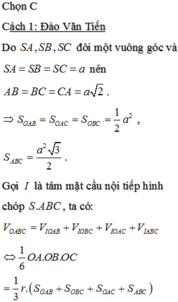Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do đó, \(SD=\dfrac{a^2}{2}:a\sqrt{2}=\dfrac{a\sqrt{2}}{4}\)
và \(AD=SA-SD=\dfrac{3a\sqrt{2}}{4}\)

Đáp án là A
Cách 1. Áp dụng công thức: r = 3 V S t p (*) và tam giác đều cạnh x có diện tích S = x 2 3 4 .
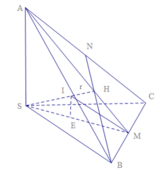
Từ giả thiết S.ABC đều có SA=SB=SC. Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng a 3 6 nên ta có SA=SB=SC=a.
Suy ra AB=BC=CA=a 2 và tam giác ABC đều cạnh có độ dài a 2 . Do đó diện tích toàn phần của khối chóp S.ABC là
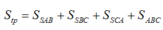
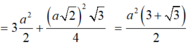
Thay vào (*) ta được:
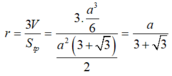

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)