Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
Đặt \(\sqrt{lnx+1}=t\Rightarrow lnx=t^2-1\Rightarrow\frac{dx}{x}=2tdt\)
\(\Rightarrow I=\int3t.2t.dt=6\int t^2dt=2t^3+C\)
\(=2\sqrt{\left(lnx+1\right)^3}+C=2\left(lnx+1\right)\sqrt{lnx+1}+C\)
\(=ln\left(x.e\right)^2\sqrt{ln\left(x.e\right)+0}\Rightarrow a=2;b=0\)
Câu 2:
\(\int\limits^b_ax^{-\frac{1}{2}}dx=2x^{\frac{1}{2}}|^b_a=2\left(\sqrt{b}-\sqrt{a}\right)=2\Rightarrow\sqrt{b}-\sqrt{a}=1\)
Ta có hệ: \(\left\{{}\begin{matrix}\sqrt{b}-\sqrt{a}=1\\a^2+b^2=17\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4\\a=1\end{matrix}\right.\) (lưu ý loại cặp nghiệm âm do \(\frac{1}{\sqrt{x}}\) chỉ xác định trên miền (a;b) dương)
Câu 4:
\(\int\frac{3x+a}{x^2+4}dx=\frac{3}{2}\int\frac{2x}{x^2+4}dx+a\int\frac{1}{x^2+4}dx\)
\(=\frac{3}{2}ln\left(x^2+4\right)+\frac{a}{2}arctan\left(\frac{x}{2}\right)+C\)
\(\Rightarrow a=2\)
\(\Rightarrow I=\int\limits^{\frac{e}{4}}_1ln\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{x}dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.lnx|^{\frac{e}{4}}_1-\int\limits^{\frac{e}{4}}_1dx=\frac{e}{4}.ln\left(\frac{e}{4}\right)-\frac{e}{4}+1=-\frac{ln\left(2^e\right)}{2}+1\)
Câu 5:
\(f'\left(x\right)=\int f''\left(x\right)dx=-\frac{1}{4}\int x^{-\frac{3}{2}}dx=\frac{1}{2\sqrt{x}}+C\)
\(f'\left(2\right)=\frac{1}{2\sqrt{2}}+C=2+\frac{1}{2\sqrt{2}}\Rightarrow C=2\)
\(\Rightarrow f'\left(x\right)=\frac{1}{2\sqrt{x}}+2\)
\(\Rightarrow f\left(x\right)=\int f'\left(x\right)dx=\int\left(\frac{1}{2\sqrt{x}}+2\right)dx=\sqrt{x}+2x+C_1\)
\(f\left(4\right)=\sqrt{4}+2.4+C_1=10\Rightarrow C_1=0\)
\(\Rightarrow f\left(x\right)=2x+\sqrt{x}\)
\(\Rightarrow F\left(x\right)=\int f\left(x\right)dx=\int\left(2x+\sqrt{x}\right)dx=x^2+\frac{2}{3}\sqrt{x^3}+C_2\)
\(F\left(1\right)=1+\frac{2}{3}+C_2=1+\frac{2}{3}\Rightarrow C_2=0\)
\(\Rightarrow F\left(x\right)=x^2+\frac{2}{3}\sqrt{x^3}\Rightarrow\int\limits^1_0\left(x^2+\frac{2}{3}\sqrt{x^3}\right)dx=\frac{3}{5}\)

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

Câu 1:
\(\int\frac{sinx}{sinx+cosx}dx=\frac{1}{2}\int\frac{sinx+cosx+sinx-cosx}{sinx+cosx}dx=\frac{1}{2}\int dx-\frac{1}{2}\int\frac{cosx-sinx}{sinx+cosx}dx\)
\(=\frac{1}{2}x-\frac{1}{2}\int\frac{d\left(sinx+cosx\right)}{sinx+cosx}=\frac{1}{2}x-\frac{1}{2}ln\left|sinx+cosx\right|+C\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=-\frac{1}{2}\end{matrix}\right.\)
\(\int cos^2xdx=\int\left(\frac{1}{2}+\frac{1}{2}cos2x\right)dx=\frac{1}{2}x+\frac{1}{4}sin2x+C\)
\(\Rightarrow\left\{{}\begin{matrix}c=\frac{1}{2}\\d=2\end{matrix}\right.\) \(\Rightarrow I=5\)
Câu 2:
\(I=\int\left(sin\left(lnx\right)-cos\left(lnx\right)\right)dx=\int sin\left(lnx\right)dx-\int cos\left(lnx\right)dx=I_1-I_2\)
Xét \(I_2=\int cos\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=cos\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\frac{1}{x}sin\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I_2=x.cos\left(lnx\right)+\int sin\left(lnx\right)dx=x.cos\left(lnx\right)+I_1\)
\(\Rightarrow I=I_1-\left(x.cos\left(lnx\right)+I_1\right)=-x.cos\left(lnx\right)+C\)
b/ \(I=\int\limits sin\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=sin\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{x}cos\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.sin\left(lnx\right)-\int cos\left(lnx\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=cos\left(lnx\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\frac{1}{x}sin\left(lnx\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x\left[sin\left(lnx\right)-cos\left(lnx\right)\right]-I\)
\(\Rightarrow I=\frac{1}{2}x\left[sin\left(lnx\right)-cos\left(lnx\right)\right]|^{e^{\pi}}_1=\frac{1}{2}\left(e^{\pi}+1\right)\)
\(\Rightarrow a=2;b=\pi;c=1\)

Câu 6:
Hoành độ giao điểm: \(\sqrt{1-x^2}=0\Leftrightarrow x=\pm1\)
\(\Rightarrow V=\pi\int\limits^1_{-1}\left(1-x^2\right)dx=\frac{4}{3}\pi\)
// Hoặc là tư duy theo 1 cách khác, biến đổi pt ban đầu ta có:
\(y=\sqrt{1-x^2}\Leftrightarrow y^2=1-x^2\Leftrightarrow x^2+y^2=1\)
Đây là pt đường tròn tâm O bán kính \(R=1\Rightarrow\) khi quay quanh Ox ta sẽ được một mặt cầu bán kính \(R=1\Rightarrow V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi\)
Câu 7: Về bản chất, đây là 1 con tích phân sai, không thể tính được, do trên miền \(\left[\frac{\pi}{6};\frac{\pi}{2}\right]\) hàm dưới dấu tích phân không xác định tại \(x=\frac{\pi}{3}\) và \(x=\frac{2\pi}{3}\), nhưng nhắm mắt làm ngơ với lỗi ra đề sai đó và ta cứ mặc kệ nó, không quan tâm cứ máy móc áp dụng thì tính như sau:
Biến đổi biểu thức dưới dấu tích phân 1 chút trước:
\(\frac{sin^2x}{sin3x}=\frac{sin^2x}{3sinx-4sin^3x}=\frac{sinx}{3-4sin^2x}=\frac{sinx}{3-4\left(1-cos^2x\right)}=\frac{sinx}{4cos^2x-1}\)
\(\Rightarrow I=\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{6}}\frac{sinx.dx}{4cos^2x-1}\Rightarrow\) đặt \(cosx=t\Rightarrow sinx.dx=-dt\)
\(\Rightarrow I=\int\limits^0_{\frac{\sqrt{3}}{2}}\frac{-dt}{4t^2-1}=\int\limits^{\frac{\sqrt{3}}{2}}_0\frac{dt}{\left(2t-1\right)\left(2t+1\right)}=\frac{1}{2}\int\limits^{\frac{\sqrt{3}}{2}}_0\left(\frac{1}{2t-1}-\frac{1}{2t+1}\right)dt\)
\(I=\frac{1}{4}ln\left|\frac{2t-1}{2t+1}\right|^{\frac{\sqrt{3}}{2}}_0=\frac{1}{4}ln\left(\frac{\sqrt{3}-1}{\sqrt{3}+1}\right)=\frac{1}{4}ln\left(2-\sqrt{3}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\\c=-1\end{matrix}\right.\) \(\Rightarrow a+2b+3c=5\)
Câu 8:
\(f\left(x\right)=\int\frac{1}{2x-1}dx=\frac{1}{2}\int\frac{d\left(2x-1\right)}{2x-1}=\frac{1}{2}ln\left|2x-1\right|+C\)
\(f\left(1\right)=1\Leftrightarrow\frac{1}{2}ln1+C=1\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\frac{1}{2}ln\left|2x-1\right|+1\Rightarrow f\left(5\right)=\frac{1}{2}ln9+1=ln3+1\)
Câu 4:
\(I=\int\limits^1_{-1}f\left(x\right)dx=\int\limits^0_{-1}f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx\)
Do \(f\left(x\right)\) là hàm chẵn \(\Rightarrow f\left(x\right)=f\left(-x\right)\) \(\forall x\)
Đặt \(x=-t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=-1\Rightarrow t=1\\x=0\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow\int\limits^0_{-1}f\left(x\right)dx=\int\limits^0_1f\left(t\right).\left(-dt\right)=\int\limits^1_0f\left(t\right)dt=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow I=\int\limits^1_0f\left(x\right)dx+\int\limits^1_0f\left(x\right)dx=2\int\limits^1_0f\left(x\right)dx=2\)
\(\Rightarrow\int\limits^1_0f\left(x\right)dx=1\)
Câu 5: Theo tính chất tích phân ta có:
\(\int\limits^{10}_0f\left(x\right)dx=\int\limits^2_0f\left(x\right)dx+\int\limits^6_2f\left(x\right)dx+\int\limits^{10}_6f\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0f\left(x\right)dx+\int\limits^{10}_6f\left(x\right)dx=\int\limits^{10}_0f\left(x\right)dx-\int\limits^6_2f\left(x\right)dx=7-3=4\)
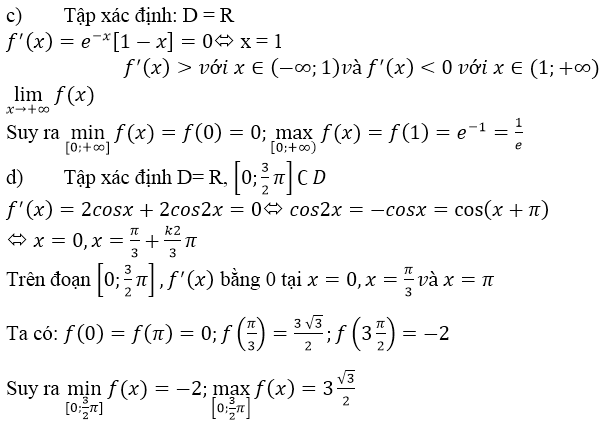
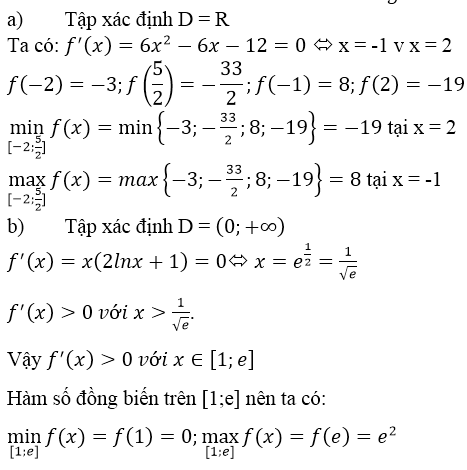

Chọn A
Ta có
Vì f(2) + f(3) + ....+f(2020) = ln a b nên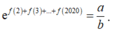
Mà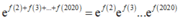
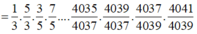
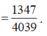
Do đó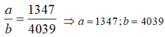
=> b = 3a = -2